1. Matrix Inverse
matrix [A]가 정방행렬이고, [A]'가 존재한다. 그런 경우, [A]' [A] = [A] [A]' = [I] 가 성립한다.

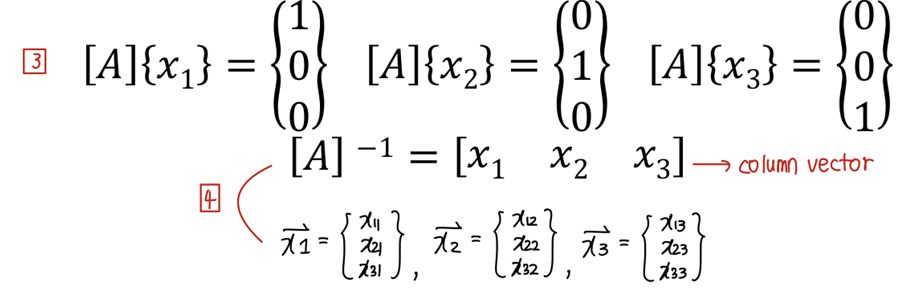
LU factorization이 여러 개의 우변 벡터(multiple right-hand-side vectors)에 대해 효율적이다. 따라서 LU factorization은 inverse 계산에도 이상적이다.

(1) Example
[A]의 inverse를 구하라.

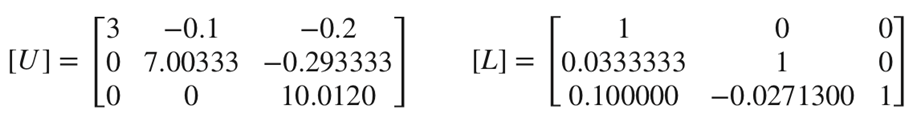
역행렬의 1열은 (1행의 값이 1인) 단위 벡터와 forward-suvstitution을 통해 구할 수 있다. 이를 통해 {d}를 구하고, {d}T를 사용하여 역행렬의 1열을 구하면 된다.

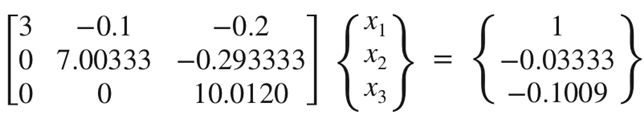
역행렬의 2열을 구하기 위해선, 아래의 공식을 사용하고 같은 순서로 {x}를 구하면 된다.

역행렬을 1열, 2열, 3열... 순서대로 하나의 열 씩 구하면 아래와 같이 채워진다.
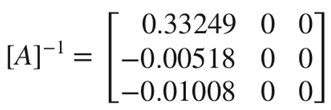


2. Vector and Matrix Norms
norm은 벡터와 행렬과 같은 multi-component mathematical entities의 크기 또는 '길이' 에 대한 측정값을 제공하는 real-valued function이다. Vector norms와 matrix norms는 다르게 계산된다.
(1) Vector norms
n size를 갖는 column vector {X}의 p-norm이다. 참고로 X는 vector를, ||X||는 verctor의 length를 의미한다.
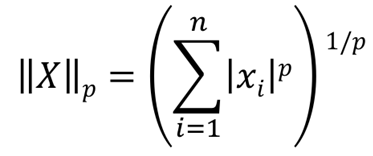
p = 2인 경우의 2-norm을 가장 많이 사용하며, 그 외에도 p = 1, p = ∞의 norm이 자주 사용된다.

우리가 잘 아는, vector의 길이는 2-norm = e-norm이다.
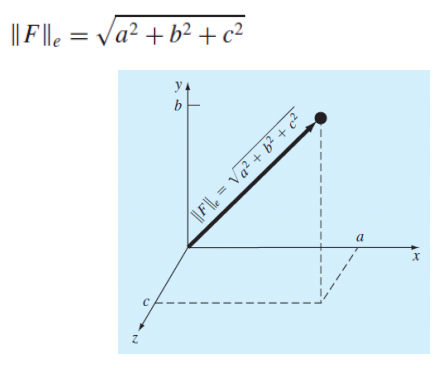
(2) Matrix norms
vector norm에 비해 흔하게 쓰이진 않지만, Euclidean norm이라 불리는 Frobenius norm을 자주 사용한다.

(3) MATLAB Commands
매트랩은 norms, condition numbers를 계산하는 built-in function이 내장되어 있다.
norm(X, p)
#% Comput the p norm of vector X
#% p can be any number, inf or 'fro' -> 그리고 Euclidean norm이다.
norm(A, p)
#% Comput the p norm of matrix A
#% p can be 1, 2, inf or 'fro' -> 그리고 Frobenius norm이다.
<요약>
-> 정방행렬의 inverse를 LU분해로 풀 수 있다.
-> matrix norm보다는 vector norm을 더 많이 사용한다.
'KNU_study > 수치해석' 카테고리의 다른 글
| 수치해석(11) Eigenvalue (1) | 2023.12.23 |
|---|---|
| 수치해석(10) Iterative Method(To solve linear system and non-linear system) (1) | 2023.12.23 |
| 수치해석(8) Gauss Elimination & LU Factorization (0) | 2023.11.02 |
| 수치해석(7) Linear Algebraic Equations and Matrices (0) | 2023.11.01 |
| 수치해석(5) Roots: Open Methods (1) | 2023.10.31 |



