1. Linear algebra and Eigenvalue
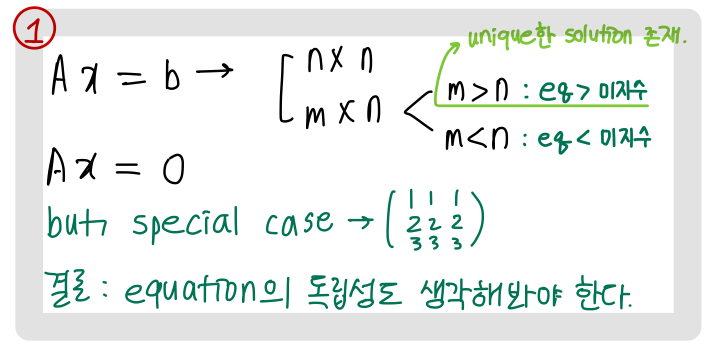


[ A ] { x } = { b }를 [1] heterogeneous system이라 하고, [ A ] { x } = 0 을 [2] homogeneous system라 한다. homogeneous system은 A의 inverse 가능 여부에 관계 없이, 항상 원점을 통과하는 solution을 가진다. 즉, A의 inverse가 존재하든 말든 Ax = 0은 해를 가진다.
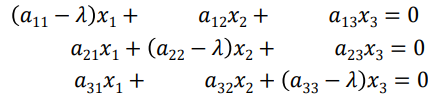
위와 같은 homogeneous system이 존재한다 하였을 때, matrix form으로 나타내면 [[𝐴] − 𝜆[𝐼]] {𝑥} = 0 이다. 이런 경우에, det([𝐴] − 𝜆[𝐼]) = 0 를 성립하게 하는 𝜆의 값을 eigenvalue라고 한다. eigenvalue와 eigenvector는 시스템의 고유한 특성이다.
(1) 예제 1
13.1 풀기 ~~
(2) 예제 2
두번째 예제를 풀자. 13.2 풀기 ~~
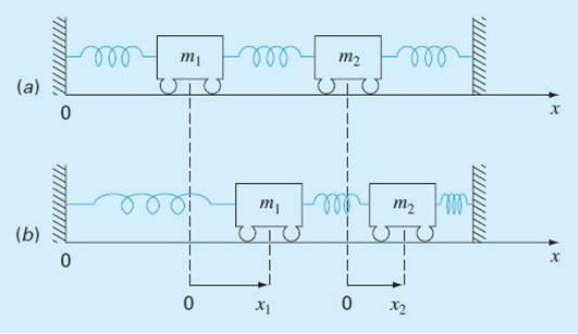
내용
(3) Solution : The Polynomial Method
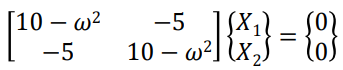
위와 같은 식이 있을 때, determinant를 계산하면 아래와 같다.
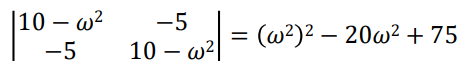
이 characteristic polynomial(특성 다항식)의 두 근은 시스템의 eigenvalue다.

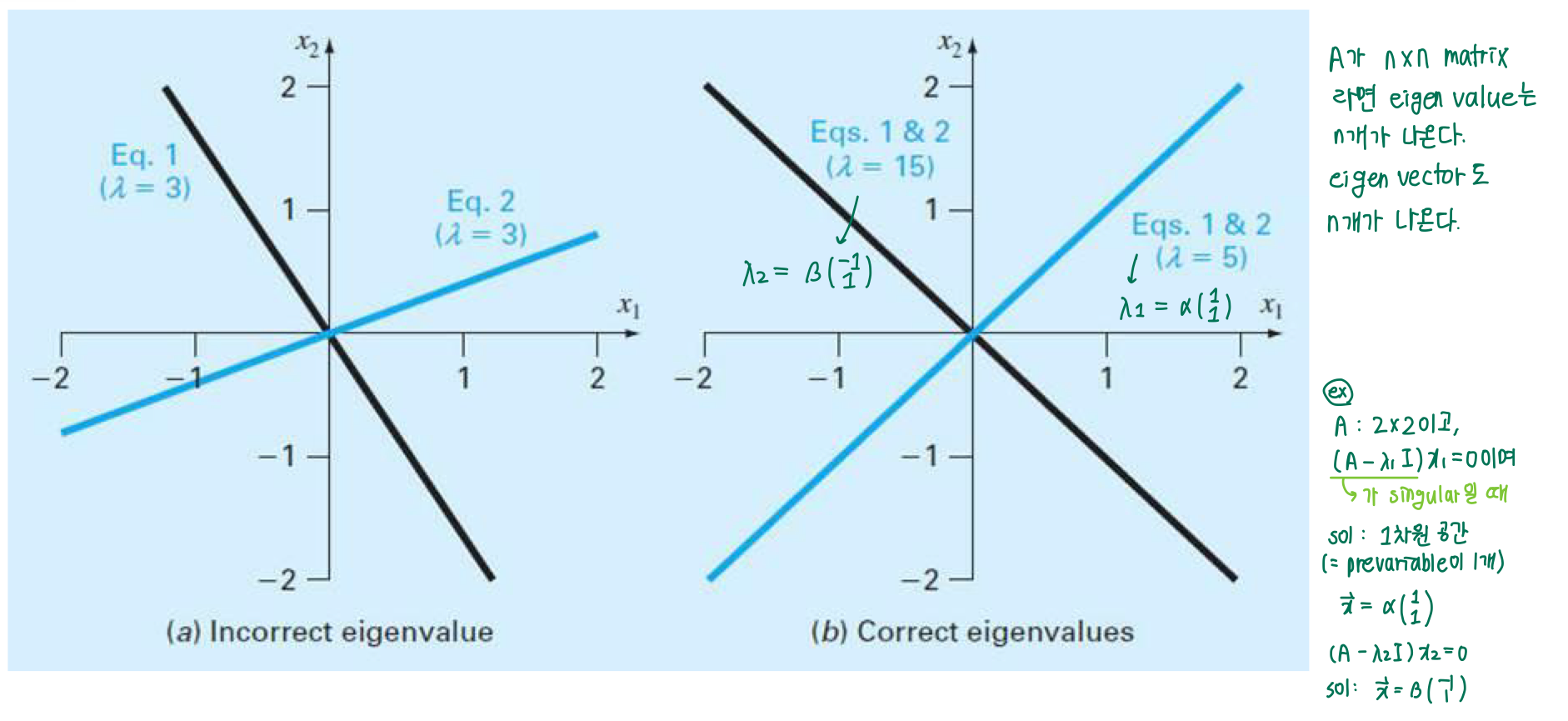
𝜔를 통해 Tp를 구하면 각각 1.62s, 2.81s가 나온다. 또한 (a) 𝜔2 = 15일 때와 (b) 𝜔2 = 5일 때 X는 열벡터 값이 나옴을 알 수 있다. 이를 그림으로 표현하면 아래와 같다.
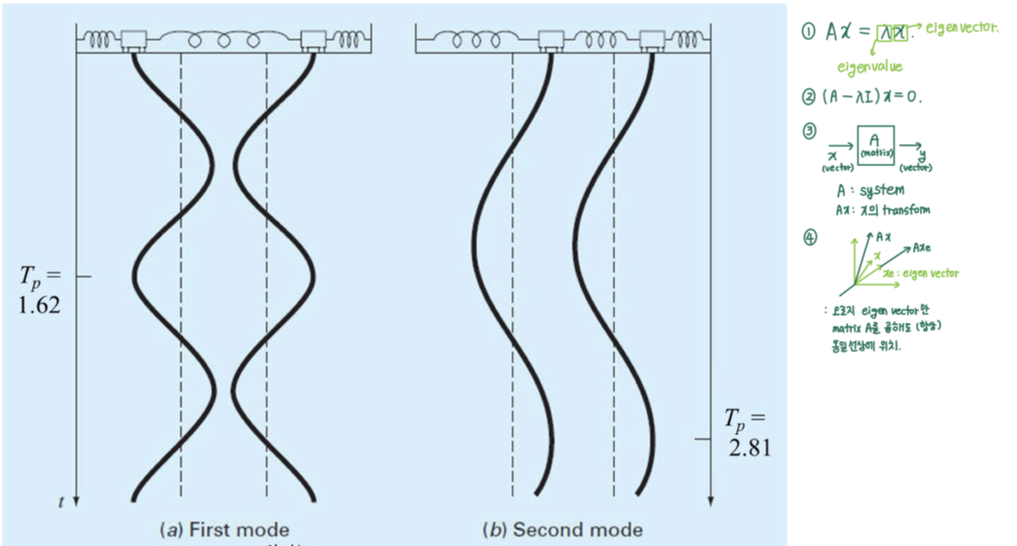
2. MATLAB code
(1) The power Method
Power method란 가장 큰 고유값을 계산하는 반복적인 방법이다.
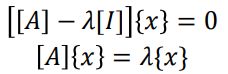
간단한 알고리즘은 아래와 같다.
function [eval, evect] = powereig(A,es,maxit)
n=length(A);
evect=ones(n,1);eval=1;iter=0;ea=100; #% initialize
while(1)
evalold=eval; #% save old eigenvalue value
evect=A*evect; #% determine eigenvector as [A]*{x)
eval=max(abs(evect)); #% determine new eigenvalue
evect=evect./eval; #% normalize eigenvector to eigenvalue
iter=iter+1;
if eval~=0, ea = abs((eval-evalold)/eval)*100; end
if ea<=es | iter >= maxit,break,end
end
(2) eigenvalue
A = [10 -5; -5; 10]
[v, lambda] = eig(A)
내용
'KNU_study > 수치해석' 카테고리의 다른 글
| 수치해석(13) Polynomial Interpolation (1) | 2023.12.23 |
|---|---|
| 수치해석(12) Linear Regression (1) | 2023.12.23 |
| 수치해석(10) Iterative Method(To solve linear system and non-linear system) (1) | 2023.12.23 |
| 수치해석(9) Matrix Inverse and Condition (0) | 2023.12.23 |
| 수치해석(8) Gauss Elimination & LU Factorization (0) | 2023.11.02 |



