1. Iterative Method
반복적 방법이란 선형시스템 Ax = b의 해를 Gauss elimination과 같이 한 번 만에 구하는 것이 아닌, 반복ㅈ거인 방법으로 초기해(solution) ... 최종해를 구하는 방법이다. 왜 갑자기 반복적 방법(Iterative method)을 배우나? 비선형 시스템에서는 해(solution)를 한번에 구하는 수치해석적 방법이 없다. 그래서, 비선형 시스템에서는 반복적 방법을 반드시 사용해야 한다. 특히 자주 나온 Newton-Raphson 방법 등이 중요하다.
(1) Gauss-Seidal Method
Gauss-Seidal Method는 선형대수 방정식 [A]{x} = {b}를 풀 때 가장 많이 사용되는 방식이다. 이는 특정 변수에 대한 시스템에서 각 방정식을 푼 다음, 나중의 방정식에서 해당 값을 사용하여 나중의 변수를 구한다. 즉, 특정 변수의 값을 구하면 바로바로 다음 방정식에 대입하여 다음 변수의 값을 순차적으로 구해나가는 원리다. 대각선이 nonzero elements인 3x3 행렬의 경우, j번째 반복값은 (j-1)번째 반복값으로부터 구한다.

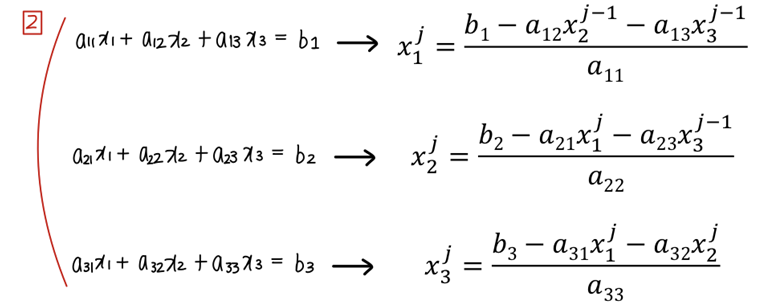

(2) Jacobi iteration
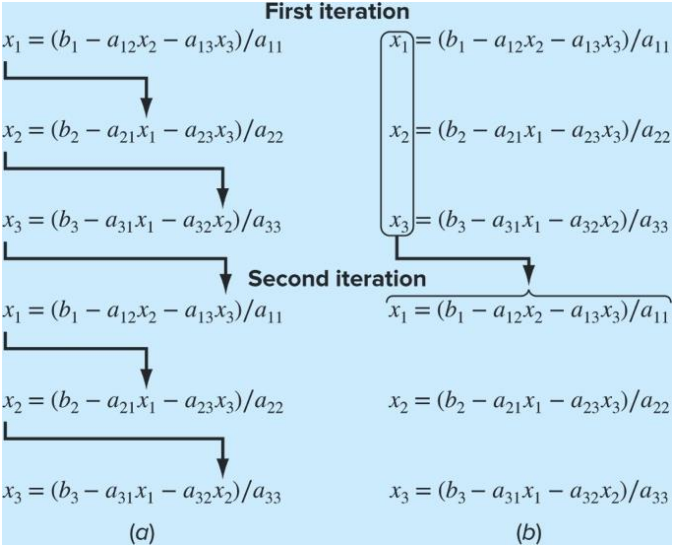
Jacobi iteration은 (1)과 유사한 방법이지만, 변수를 바로바로 업데이트하지 않고 몰아서 스텝마다 한 번씩만 업데이트한다.
(3) Convergence
iterative method의 수렴은 {x}에서 각 요소의 상대적인 백분율 변화를 결정함으로써 계산될 수 있다. 예를 들어 j번째 반복에 있는 i번째 요소의 경우는 아래 식과 같다.
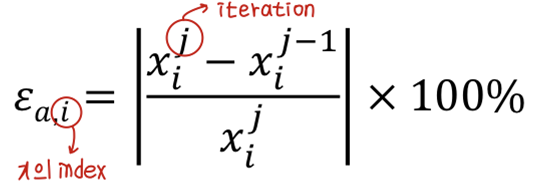
이 방법은 모든 element들이 설정된 허용 오차(set tolerance)로 수렴되면 종료된다.
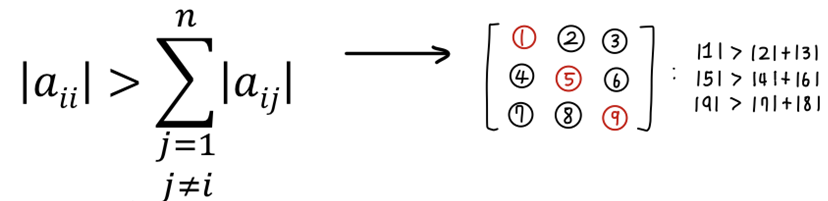
Gauss-Seidal 방법은 발산할 수 있지만, 만약 시스템이 diagonally dominant하다면, 이는 반드시 수렴할 것이다. Diagonal dominance는 대각 원소의 절대값은 대각 원소 이외 원소의 절대값의 합보다 크다는 것을 의미한다. 아래의 식을 참고하자. 그리고 예제 12.1을 풀자.
(4) Relaxation
Relxation이란 수렴(convergence)을 높이기 위한 방법으로, 특정 반복에서의 값이 이전의 값과 새로 계산된 값의 조합으로 구성된 것이다. λ는 0과 2 사이의 값을 가지는 weighting factor이다.


적절한 λ을 선택하는 것은 case-by-case다.
정리하자면 (1)은 무조건 새로 계산된 값을 사용하고, (2)는 이전의 값을 사용하여 한 세트를 다 구한 후 업데이트 하며, (4)는 새로 계산된 값과 이전의 값을 적절히 같이 사용한다.
(5) examples
아래의 식을 overrelaxation( λ = 1.2 )을 사용하여 Gauss-Seidel 방식으로 풀어라. stopping criterion은 10%.

diagonally dominant가 되도록 방정식을 재배열하자. 그리고 x1, x2에 대해 각각 식을 풀자.
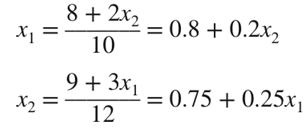
첫번째 반복에서, x1 = x2 = 0이라는 초기값을 사용하여 x1을 구한다. 구해진 x1을 대입하여 x2를 구하기 전에, overrelaxation을 통해 수정된 x1 값을 구하고, 그 수정된 값을 대입하여 x2를 구하자.

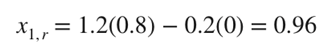
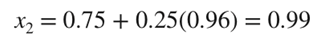
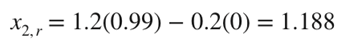
우리가 초기값 0에서부터 시작해서 아마 error가 거의 100%일 것이다. 그러므로 두 번째 반복을 진행하자.

첫 번째 반복과 같은 과정을 거친다. 아직도 stopping criterion에 만족하지 못하므로, 몇 번 더 반복한다.

다행히 3번째 반복에서, stopping criterion 이내에 들었으므로 반복을 종료한다. 결과적으로 x1 = 0.984177, x2 = 0.999586으로 정확한 해인 x1 = x2 = 1에 수렴하는 것을 알 수 있다.
2. Nonlinear systems
Nonlinear systems 역시 Gauss-Seidal method와 같은 방식으로 풀 수 있다. unknowns 중 하나의 해를 구하고, 이전 반복 정보를 사용하여 unknown을 업데이트하는 이러한 방식을 successive substitution이라 한다.
(1) example

첫번째 방식대로 x1을 표현하면 발산함을 알 수 있다.
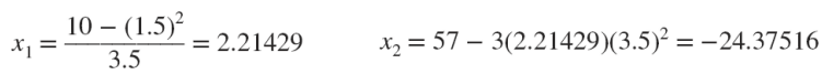
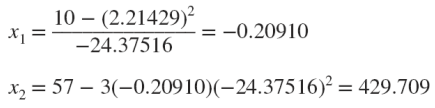
다른 equation format을 사용하면, 결과를 수렴할 것이다.
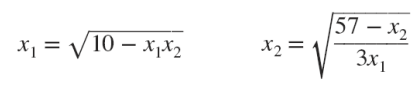
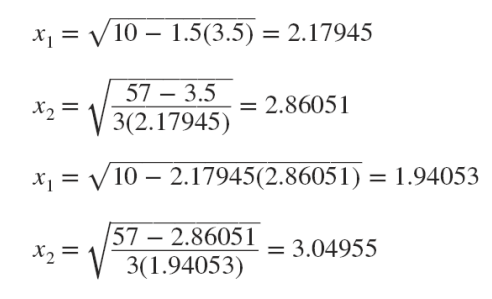
(2) Newton-Raphson
비선형 시스템은 여러 변수에 대해 Newton-Raphson 방식을 사용하여 해결할 수 있다. 아래는 1차 테일러 급수를 확장한 식이다. 여기서 xi는 루트에서의 초기 추측이고, xi+1는 기울기가 x축을 가로채는 지점이다.
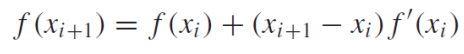
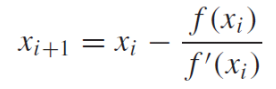
single nonlinear equation은 f(x) = 0으로 표현할 수 있다. multiple nonlinear equation은 아래와 같이 표현된다. 따라서 해는 아래의 모든 방정식을 0으로 만드는 x 값이다.
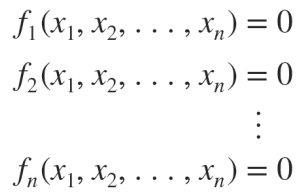
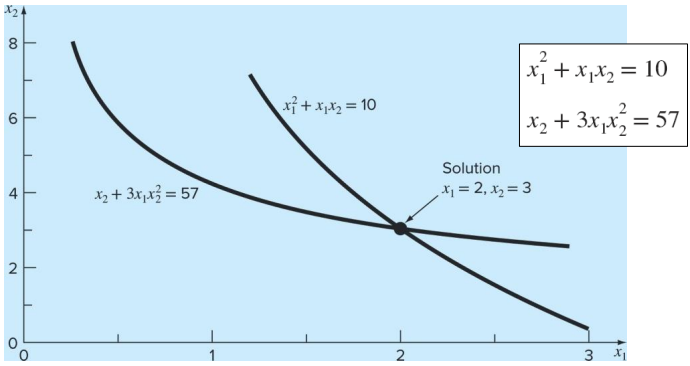
예시를 들어보자. (1)의 식에서 해를 구하려면, 두 식을 모두 만족하는 x1, x2를 구해야 한다.
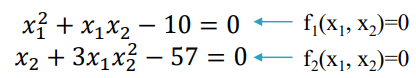
2변수 시스템에서(two-variable system), 테일러 급수 근사치와 뉴턴-랍슨 방정식은 다음과 같다.
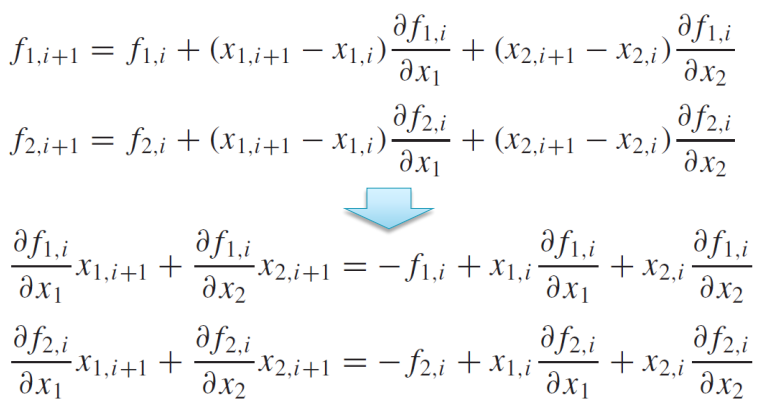
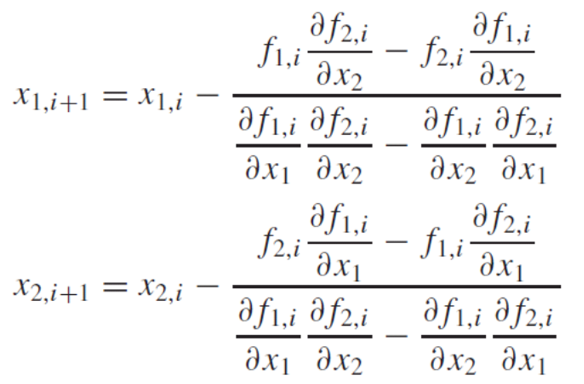
(2) MATLAB's Function
fsolve function의 문법은 아래와 같다.
[x, fx] = fsolve(function, x0, options)
#% [x, fx] : 근 x를 포함하는 벡터, 근에서 평가된 함수의 값을 포함하는 벡터
#% function : 함수
#% x0 : unknowns에 대한 초기 추측들을 가진 벡터
#% options : optimset 함수에 의해 생성된 데이터 구조
#% options를 사용하지 않으려면 빈 벡터 []를 대신 작성한다.
#example
function f = fun(x)
f = [x(1)^2+x(1)*x(2)-10;x(2)+3*x(1)*x(2)^2-57];
clc, format compact
[x,fx] = fsolve(@fun,[1.5;3.5])
(3) Jacobian Matrix
Jacobian Matrix는 함수 f1, f2, f3...와 변수 x1, x2, x3...의 편미분으로 구성된다.
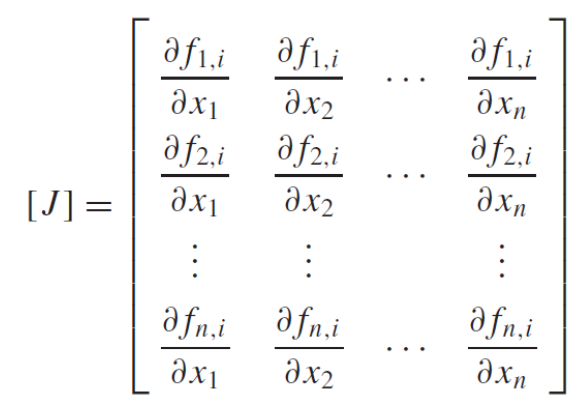
Newton-Rapgson method를 Jacobain Matrix를 사용하여 풀어보자.


나머지는 예제를 풀며 이해하자 ..^^
'KNU_study > 수치해석' 카테고리의 다른 글
| 수치해석(12) Linear Regression (1) | 2023.12.23 |
|---|---|
| 수치해석(11) Eigenvalue (1) | 2023.12.23 |
| 수치해석(9) Matrix Inverse and Condition (0) | 2023.12.23 |
| 수치해석(8) Gauss Elimination & LU Factorization (0) | 2023.11.02 |
| 수치해석(7) Linear Algebraic Equations and Matrices (0) | 2023.11.01 |



