728x90
반응형
1. Special Matrices
m = n인 행렬을 정방행렬이라고 한다. 아래는 또다른 다양한 종류의 행렬들이다.

2. Matrix Operations
(1) Matrix Multiplication
차원별로 각각 곱해서 더하고 ~~ 하면 된다.
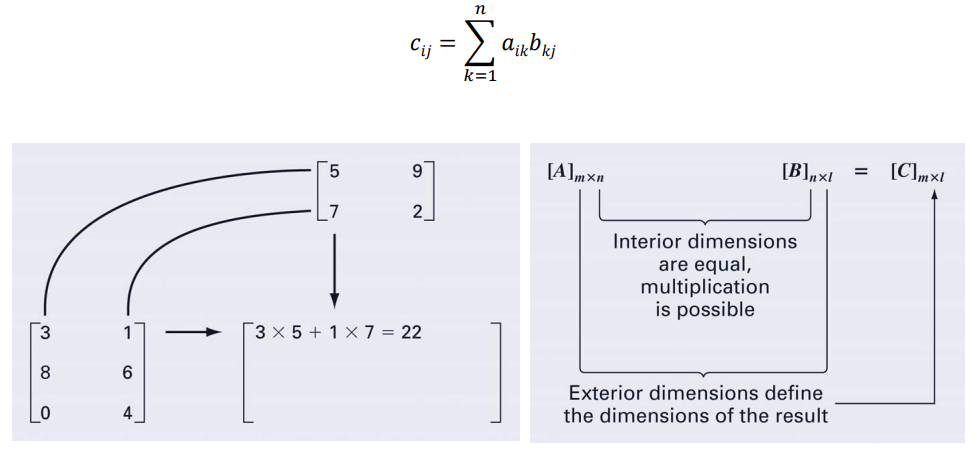
(2) Matrix Inverse and Transpose
Matrix Inverse는 y = Ax에서 행렬 A가 [1] square matrix면서 [2] nonsingular이어야 한다. 매트랩에선 inv(A)를 사용한다. 다음으로 Matrix Transpose는 mxn이 nxm이 되는 것으로, 매트랩에선 A'라고 표현한다.

3. Representing Linear Algebra
매트랩은 다음의 방정식들을 행렬로 표현한다. 참고로 algebraic eqaution을 푸는 방법에는 2가지가 있는데, [1] Left-division(x = A\b)과 [2] Matrix inversion(x = inv(A)*b)이 그에 해당한다.
16페이지 예시를 풀어보자.

728x90
반응형
'KNU_study > 수치해석' 카테고리의 다른 글
| 수치해석(9) Matrix Inverse and Condition (0) | 2023.12.23 |
|---|---|
| 수치해석(8) Gauss Elimination & LU Factorization (0) | 2023.11.02 |
| 수치해석(5) Roots: Open Methods (1) | 2023.10.31 |
| 수치해석(4) Roots: Bracketing Methods (0) | 2023.10.31 |
| 수치해석(3) Roundoff and Truncation Errors (1) | 2023.10.31 |



