1. Gauss Elimination
Ax=b를 풀 것이다. 푸는 방법은 두 가지, [1] x = A\b로 풀거나 [2] x = inv(A)*b로 푸는 것이다. 두 번째의 경우, 행렬 A는 정방행렬이면서도 nonsingular를 만족해야 한다.
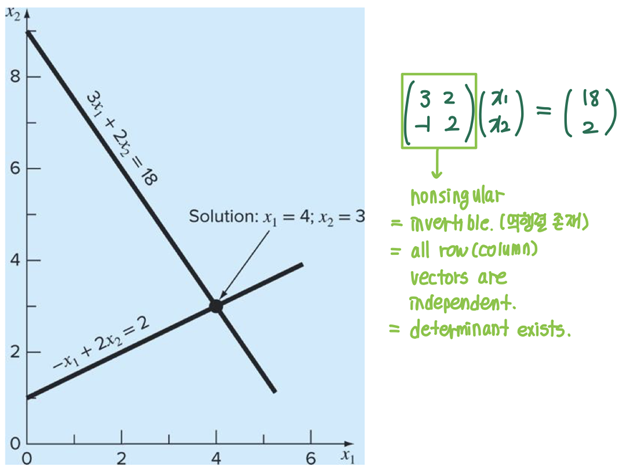
(1) Graphical method
(a)의 경우 no solution이고, (b)의 경우 무한한 해가 존재하며 (c)의 경우 roundoff error와 같은 ill-conditioned 상태다.

(2) Determinants
D = |A|는 nxn 행렬에 따라 아래와 같은 공식으로 풀면 된다.

(3) Cramer's Rule
선형대수 방정식 체계에서 알려지지 않은 각각은 미지수 계수의 열을 상수 b1, b2, ... bn으로 대체함으로써 분모 D와 D에서 얻은 분자로 표현할 수 있다.
24쪽 예시를 풀어보자.

(4) Naive Gauss Elimination
대규모 시스템의 경우, 크래머의 룰이 실행 불가능할 수 있다. 대신 forward elimination followed by back substitution을 사용하여 방정식에서 미지수를 제거하는 순차적 과정이 사용된다. 이것이 가우스 소거다.
[1] Forward elimination에서는 upper triangular matirx 형태로 소거를 한다. [2] Back substitution에서는 마지막 행부터 시작하여 점차 올라가며 해를 구한다.
예제 9.3를 찾아서 풀어보자.

(5) Gauss Program Efficiency
가우스 소거의 실행은 floating-point operations에 의존한다. nxn matrix의 flop count는 아래와 같다.

결론적으로, 시스템이 커질수록 계산 시간은 점차 증가한다. 대부분 elimination 단계에서 시간이 소요된다.
(6) Pivoting
대각선을 따라 있는 계수가 0이거나 0에 가까운 경우 naive Gauss eliminatino 문제가 발생한다. 그냥 행들끼리 순서를 바꿔주면 된다. 바꿔줄 때 가장 큰 절대값을 갖는 계수를 1행으로 바꾼다. 이렇게 부분적으로 행 전환하는 것을 partial pivoting이라고 한다. 만약 피벗 요소의 오른쪽 행도 확인하고 열을 전환하면, 이를 complete pivoting이라 하는데 뭐 굳이 이해할 필요는 없다.

(7) Tridiagonal Systems
tridiagonal system은 대역폭이 3인 밴드형 시스템이다. 이는 가우스 제거로 풀 수 있지만, 대부분의 행렬 요소가 이미 0이기 때문에 훨씬 적은 노력으로도 풀 수 있다.
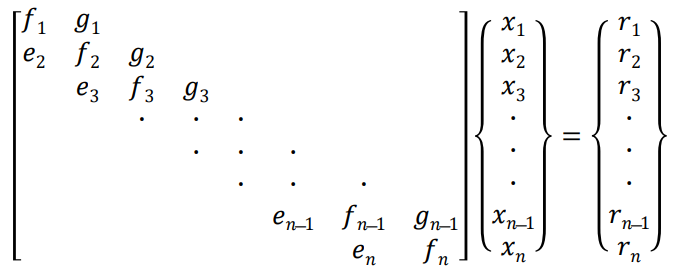
우선 행렬을 upper triangular form으로 변환한다. 이를 위해 첫 번째 방정식에 e2/f1을 곱하고, 두 번째 방정식에서 결과를 빼서 행한다.
2. LU Factorization
Factorization, decomposition이라 하는 이 계산은 Ax = b를 구하기 위한 계산 방법 중 하나다. 보통 LU factorization, QR factorization을 많이 사용한다. Ax = b를 [L][U]{x} = {b}로 변경하는 흐름이며 행렬 A, L, U모두 nxn 크기를 가진다.
(1) LU Factorization
두 가지 단계다. [1] 행렬 A를 lower triangular matrix [L]과 upper triangular matrix [U]의 곱으로 분해하기 위해 인수분해(factorization)를 실시한다. 참고로 [L]은 대각선의 각 항목에 대해 1을 갖는다. [2] {x}를 풀기 위해 Substitution을 수행한다. 가우스 제거는 LU 인수분해를 이용하여 대체될 수 있다.
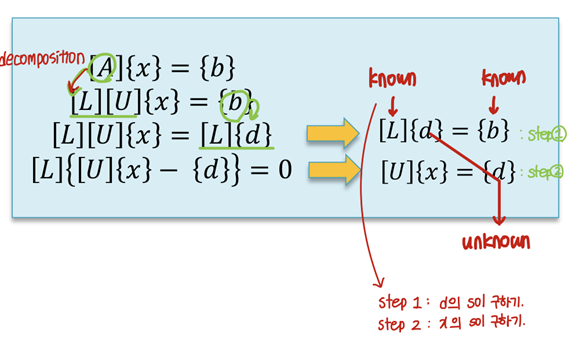

(2) Gauss Elimination as LU Factorization
매트랩에서 LU Factorization을 구현해보자. 코드는 아래와 같다.
[L, U] = lu(A)
d = L/b
x = U/d
(3) Cholesky Factorization
Symmetric matrix(대칭 행렬)에 사용할 수 있는 솔루션 기술이다. 대칭 행렬은 아래와 같이 분포한다는 사실에 기초하며 [A] = [A]T, 여기서 T는 전치 행렬을 의미한다. 나머지 공정은 LU 분해 및 Gauss 제거와 유사하지만, 오직 하나의 행렬인 [U]만 저장하면 된다. 문제 공식은 다음과 같다.
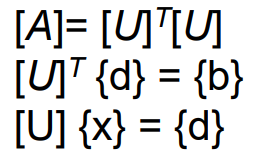
예제를 와르를 풀어보자.
'KNU_study > 수치해석' 카테고리의 다른 글
| 수치해석(10) Iterative Method(To solve linear system and non-linear system) (1) | 2023.12.23 |
|---|---|
| 수치해석(9) Matrix Inverse and Condition (0) | 2023.12.23 |
| 수치해석(7) Linear Algebraic Equations and Matrices (0) | 2023.11.01 |
| 수치해석(5) Roots: Open Methods (1) | 2023.10.31 |
| 수치해석(4) Roots: Bracketing Methods (0) | 2023.10.31 |



