1. Open Methods
Open Methods는 [1] 하나의 시작값 또는 [2] 루트를 브라켓화할 필요가 없는 두 개의 시작값만을 요구한다. 계산이 진행됨에 따라 발산할 수 있지만, 수렴할 때 보통 Bracket Methods보다 훨씬 더 빠르게 수행된다.

(1) Simple Fixed-Point Iteration
Simple Fixed-Point Iteration Methods의 순서는 다음과 같다. [1] x가 식의 왼쪽에 있도록 함수 f(x) = 0을 재배열한다. [2] x = g(x)로 두고, 새로운 함수 g를 사용하여 x의 새로운 값인 xi+1 = g(xi)를 예측한다. 대략화된 오류 식은 아래와 같다.

예제를 풀어보겠다. 엄청 간단하다. f(x) = 0으로 두고, 좌변에 x만을 남기면 된다. x = e-x의 방법도 있지만, 만약 e-x = x를 할 경우 x = -ln(x)가 되는 것이다.


(2) Convergence of the simple fixed-point iteration
Simple fixed-point iteration 방법의 수렴은 근에 가까운 g'(x)가 1보다 작은 크기를 가져야 한다.

예제를 풀어보겠다. 엄청 간단하다. x = 1 + 0.5sinx의 경우, g'(x) = 0.5cosx로, |g'(x)|<=1/2이다. 따라서 해당 함수는 수렴한다. x = 3 + 2sinx의 경우, g'(x) = 2cosx로, |g'(x)|>1이다. 따라서 해당 함수는 발산한다. 위에서 보았듯이 거미줄 모양의 그림을 그리면 수렴하는 것이고, 아래 그림들과 같으면 발산한다.

(3) Newton-Raphson Method
Newton-Raphson Method란 모든 root-locating 공식들 중에서 가장 널리 사용되는 방법으로, 순서는 다음과 같다. [1] 임의의 x에서 f(x) 곡선에 대한 접선을 형성한 다음, [2] 접선을 따라 x축과 교차하는 위치로 이동한다. [3] 근에 수렴할 때까지 이를 반복한다.


이 방법의 [1] 장점은 (i+1) 반복의 오차는 i의 오차 제곱에 대략 비례한다는 것이다. 이것을 quadratic convergence(2차 수렴)이라고 한다.
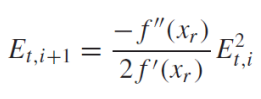
[2] 단점은, 근을 찾는 과정이 느리거나, 발산할 수 있다는 것이다. 이를 해결하기 위해, 최대한 root과 가깝게 초기값을 지정해야 한다. 아래는 근 찾기를 실패한 그림들이다.
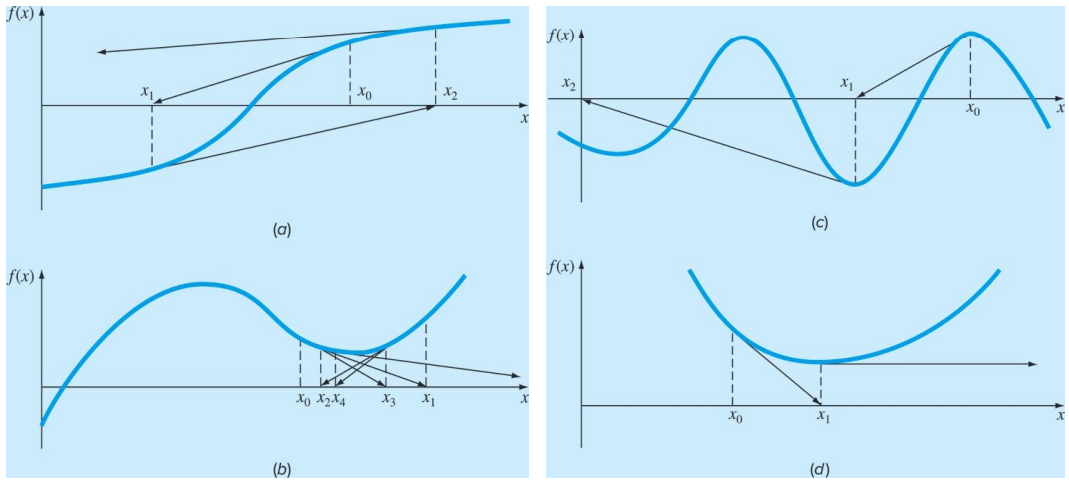
예제를 풀어보겠다. 엄청 간단하다. f(x) = ex-x의 경우, 아까 언급한 공식에 집어넣으면 된다.

예제를 풀어보겠다. Use the M-file function to determine the mass of the bungee jumper with a drag coefficient of 0.25 kg/m to have a velocity of 36m/s after 4s of free fall. The acceleration of gravity is 9.81.
#% 뉴턴-랩슨 방법을 사용하여 근사 해를 찾는 방법.
function [root, ea, iter] = newtraph(func, dfunc, xr, es, maxit, varagin)
if nargin<3, error('at least 3 input arguments required'), end
if nargin<4|isempty(es), es=0.0001; end
if nargin<5|isempty(maxit), maxit=50; end
iter=0;
while(1)
xrold=xr;
#% 뉴턴-랩슨 공식에 따라 새로운 추정값 'xr'을 계산한다.
xr=xr-func(xr)/dfunc(xr);
iter=iter+1;
#% 'xr이 0이 아니라면, 추정 상대 오차 'ea'를 계산한다.
if xr ~= 0, ea=abs((xr-xrold)/xr)*100; end
if ea <= es|iter>=maxit, break, end
end
#% 최종 근사해 'xr'을 반환한다.
root=xr;

(3) Secant Method
Newton-Raphson 방법을 구현할 때의 문제점은 도함수가 어렵거나 계산하기 어려운 특정 함수가 있다는 점이다. 이러한 경우, Secant Method를 사용하여 backward finite divided difference에 의해 도함수를 근사화할 수 있다.

이러한 근사치를 (2)에 대입하면, 아래 공식들을 얻을 수 있다. 참고로, 이 방법은 도함수를 분석할 필요는 없지만, 초기 x 추정치가 2개 필요하다는 단점을 가진다.

(4) Modified Secant Method
도함수 추정을 위해 2개의 임의의 값을 사용하는 대신 대안적인 접근법은, f'(x)를 추정하기 위해 독립 변수의 fractional perturbation을 사용한다. 즉, 아래 공식에서 δxi를 아주 작은 값으로 생각하는 것이다.

예제 6.5를 풀어보자. Modified secant method를 사용하여 4초 자유낙하 후에, 속도 36m/s를 갖고, 항력계수 0.25kg/m을 갖도록 번지점프대의 질량을 결정하자. 중력 가속도는 9.81m/s2이며, perturbation fraction에 대해 50kg의 초기 추측과, 10-6의 값을 사용한다.

2. MATLAB's Function
(1) fzero Function
매트랩의 fzero는 주어진 함수 'function'의 근을 찾는 데 사용되고, bracketing 방법과 open 방법 둘 다에게 최고의 품질을 제공한다. 아래와 같이, x0과 x1을 제외하고는 부호 변경을 괄호로 묶어야 한다.
#% x0 : 초기 추정값, 근을 찾기 시작할 위치.
#% x : root의 위치.
#% fx : 해당 root에서 평가된 함수.
#% options : 옵션 구조체.
#% function : 근을 찾을 함수.
#% 'fzero' 함수는 근과 해당 근에서의 함수 값인 'fx'를 반환한다.
x = fzero(function, x0, options)
[x, fx] = fzero(function, x0, options)
#% 사용 예시
x = fzero(function, [x0 x1])
[x, fx] = fzero(function, [x0 x1])
Options는 세 번째 입력 인수로, 0으로 전달될 수도 있다. 이는 optimset 명령에 의해 생성된 데이터 구조이며, 코드는 아래와 같다. fzero에서 일반적으로 사용되는 매개 변수인 [1] 'display'는 'iter'로 설정하면 모든 반복에 대한 상세한 기록이 표시되며 [2] 'tolx'는 x에 종료 허용 오차를 설정하는 양의 스칼라다.
예제를 풀어보겠다. fzero를 사용하여 x=0.5의 초기 추측으로 시작하는 f(x) = x10 - 1의 근을 찾자. 매트랩은 35개의 function 카운트를 수행한 후 x=1, fx=0을 보고할 것이다.
#% parn : 설정한 파라미터 이름들.
#% valn : 해당 매개 변수에 설정할 값.
options = optimset(‘par1’, val1, ‘par2’, val2,…)
#% [1]의 예제
options = optimset(‘display’, ‘iter’);
[x, fx] = fzero(@(x) x^10-1, 0.5, options)
또한, 덜 엄격한 허용 오차를 사용한다고 가정하자. 이러한 경우 우리는 optimset 함수를 사용하여 낮은 최대 허용 오차, 덜 정확한 근 결과 추정치를 설정할 수 있다.
#$ [2]의 예제
options = optimset('tolx', 1e-3);
[x, fx] = fzero(@(x) x^10-1, 0.5, options)
(2) Polynomials
Polynomials는 일반적인 형태의 비선형 대수 방정식의 특별한 유형이다. 매트랩에는 허수, 복소수를 포함한 다항식의 모든 근을 결정하는 roots라는 프로그램이 내장되어 있다.
#% x : 근을 포함하는 열 벡터
#% c : 다항식 계수를 포함하는 행 벡터
x = roots(c)
#% 예제
x = roots([1 -3.5 2.75 2.125 -3.875 1.25])
만약 근이 주어진 경우라면, 매트랩의 poly 함수를 사용하여 다항식 계수를 결정할 수 있다.
#% 예제 : x = 0.5 및 x = -1에 대해 f(x) = 0인 f(x)를 찾자.
#% 매트랩은 b = [1.0 0.5 -0.5]를 출력할 것이다.
#% 이는 f(x) = x2 + 0.5x - 0.5에 해당한다.
b = poly([0.5-1])
매트랩의 polyval 함수는 다항식을 1개 이상의 점에서 평가할 수 있다.
#% 예제
#% 이는 f(1)을 계산하는데, 매트랩은 이를 -0.25로 보고한다.
a = [1 -3.5 2.75 2.125 -3.875 1.25];
polyval(a, 1)
'KNU_study > 수치해석' 카테고리의 다른 글
| 수치해석(8) Gauss Elimination & LU Factorization (0) | 2023.11.02 |
|---|---|
| 수치해석(7) Linear Algebraic Equations and Matrices (0) | 2023.11.01 |
| 수치해석(4) Roots: Bracketing Methods (0) | 2023.10.31 |
| 수치해석(3) Roundoff and Truncation Errors (1) | 2023.10.31 |
| 수치해석(2) MATLAB 실습 (2) | 2023.10.28 |



