1. Error
(1) Sources of Solution Error
컴퓨터로 수치 모델 문제를 풀 땐 유한한 차이로 속도의 도함수를 근사해야 한다. solution은 정확하지 않다. 즉, 오류가 발생한다. 컴퓨터는 디지털 기기이기 때문에, 숫자 크기와 정밀도를 나타내는 능력에 한계가 있다.

(2) Accuracy and Precision
계산 및 측정과 관련된 오류는 정확도 및 정밀도와 관련하여 특성화할 수 있다. [1] 정확도(Accuracy)는 계산된 값 또는 측정된 값이 실제 값과 얼마나 밀접하게 일치하는지를 의미한다. [2] 정밀도(Precision)는 계산된 값 또는 측정된 값들끼리 서로 얼마나 밀접하게 일치하는지를 의미한다.
| Predicted conditon | Predicted condition | ||
| Total population = P + N |
Positive(PP) | Negative(PN) | |
| Actual condition | Positive(P) | True positive (TP) -> hit |
False negative (FN) -> type II error, miss |
| Actual condition | Negative(N) | False positive (FP) -> type I error, false alarm |
True negative (TN) -> correct rejection |

(3) Error Definitions
True error(Et)란 참값과 근사값의 차이를 의미한다. Absolute error(절대오차, |Et|)란 참값과 근사값의 절대차를 의미한다. True fractional relative error란 true error를 'true' 값으로 한 번 더 나눈 값이다. 또한 Relative error(εt)란 true fractional relatibe error를 백분율로 표현한 것이다.

approximate percent relative error는 근사 오차를 근사로 나눈 값으로, 백분율로 표시할 수 있다. 여기서 근사값(approximation)은 True 값을 알 수 없는 경우에 true에 최대한 가깝다고 가정하는 값을 말한다.

iterative process(반복 공정)인 경우, 오차는 연속적인 반복 간의 값 차이로 근사화될 수 있다.

(4) Using error estimates
계산을 수행할 때 오차 부호에 관심을 두지 않고, 백분율 기준으로 오차의 절대값이 미리 지정된 허용 오차 εs보다 낮은지의 여부에만 관심을 가지는 경우가 많다. 이러한 경우, 계산은 다음과 같이 반복된다. 또한 이러한 조건 관계를 stopping criterion이라고 한다.

하나의 예시로, 아래의 식을 이용하여 e0.5를 컴퓨터로 계산해보자. 코드는 그 아래와 같다.

#% 3개의 입력 인수를 받고, 3개의 출력 값 반환.
function [fx, ea, iter] = IterMeth(x, es, maxit)
if nargin < 2 | isempty(es), es = 0.0001; end
if nargin < 3 | isempty(maxit), maxit = 50; end
#% iter : 반복 횟수, sol : 현재 근사값, ea : 근사 오차
iter = 1; sol = 1; ea = 100;
while(1)
solold = sol;
sol = sol + x^iter/factorial(iter);
iter = iter + 1;
#% 'sol'이 0이 아니라면, 근사 오차 'ea'를 계산한다.
if sol ~= 0
ea = abs((sol-solold)/sol)*100;
end
if ea <= es | iter >= maxit, break, end
end
#% 최종 근사값 'sol'을 출력 변수 'fx'에 저장한다.
fx = sol;
end
2. Roundoff Error
(1) Roundoff Errors
Roundoff error는 디지털 컴퓨터가 일부 양을 정확하게 나타낼 수 없기 때문에 발생한다. 수치 계산과 관련된 반올림 오류의 주요한 두 가지 측면이 있다. [1] 디지털 컴퓨터는 숫자를 표현하는 능력에 크기, 정밀도 제한이 있다. [2] 특정 수치 조작은 roundoff error에 매우 민감하다.
(2) Integer represetation
16비트 워드 크기를 가정할 때 부호에 1비트가, 이진 정수를 표현하는 데 15비트가 사용된다.
| 16 - bit word | (1x20) + (1x21) + (1x22) ... + (1x215) = 32,767 |
| n - bit word | possible range : -2n-1 to 2n-1 -1 |
(3) Floating-point representation
5-digit word, base-10 computer가 부호에 1디지트, 지수에 2디지트, 가수(mantissa)에 2디지트 사용된다.
지수, 가수가 무엇인가? 부동 소수점 숫자는 일반적으로 두 부분으로 나누어진다. [1] 가수란? 실제 숫자 값의 부분으로, 숫자의 정확한 값을 나타낸다. 가수는 소수점 이상 또는 이하의 숫자를 나타내며, 이진수로 표현된다. 예를 들어 0.75를 이진으로 표현하면 가수는 0.11이다. [2] 지수란 숫자의 소수점을 어디에 위치시킬지 나타내는 부분으로, 숫자의 크기 및 범위를 제어한다. 이 두 부분은 함께 사용되어 숫자를 표현한다.

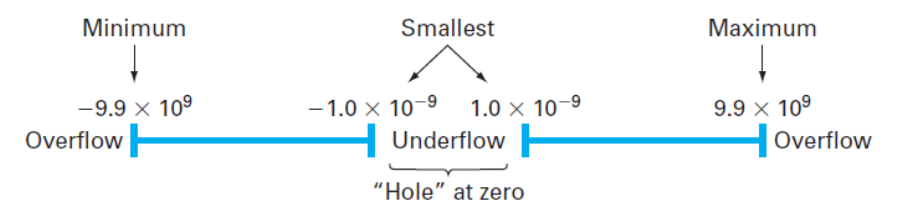
(4) Computer Number representation
기본적으로 매트랩은 부동 소수점 숫자를 나타내기 위해 8바이트(64비트)가 사용되는 IEEE 이중 정밀도 형식이다. 부호는 1bit, mantissa f는 52bit, exponent e는 11bit가 사용되었다. exponent range는 -1022부터 1023까지다. (-1023, -1024는 특수 목적으로 사용된다.)
매트랩이 저장할 수 있는 가장 큰 정수는 .. 소수 표현 파트는 나중에 더 자세히 공부해보자.

(5) Roundoff Error, Truncation Error 예제
내용
3. The Taylor Theorem and Series
Taylor theorem은 임의의 매끄러운 함수가 다항식으로 근사될 수 있음을 나타낸다. 테일러 시리즈는 이 아이디어를 수학적으로 표현하게끔 하는 수단이다. 공식은 아래와 같다.

Taylor theorem을 또다르게 표현한다면 아래의 식이 성립한다. 여기서 a = 0으로 두면 그 아래와 같다. a = 0인 경우를 Maclaurin series 또는 구별하지 않고 Taylor series라고 부른다.


(1) Truncation Error
일반적으로 n차 테일러 급수의 확장은 n차 다항식에서 정확하다. 다른 경우, 나머지 항 Rn은 hn+1의 차수이며 [1] term을 많이 사용할수록 오차가 작아지며, [2] 간격이 작을수록 지정된 항 수에 대한 오차가 줄어든다.

0차 항 이후에 테일러 급수 확장을 절단하여 산출했다고 가정해보자. 이 예측의 나머지(오차)는 절단된 나머지 항으로 구성된다. 그림을 보면 이해가 갈 것이다.
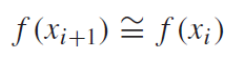
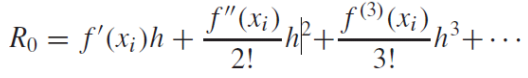

(2) Numerical Differentiation
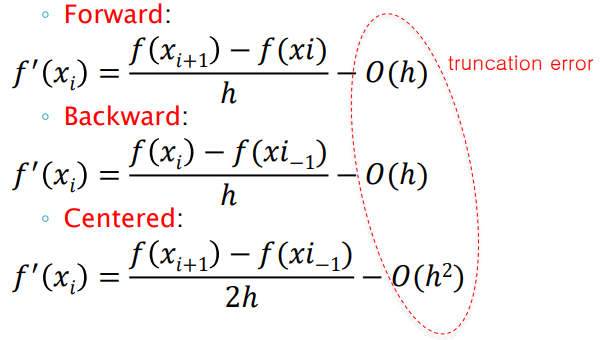
1차 테일러 급수를 사용하여 도함수에 대한 근사치를 계산할 수 있다. 이는 i와 i+1의 데이터를 활용하여 도함수를 추정하기 때문에 [1] forward difference라고 한다. 이 외에도 사용된 점에 따라 [2] backward difference는 Taylor 시리즈를 뒤로 확장하여, 현재 값을 기준으로 이전 값을 계산하는 방법이다. truncation error는 O(h)이다. [3] centered difference는 정방향 테일러 급수 전개에서 방정식을 뺀 값으로, truncation error는 O(h2)이다.
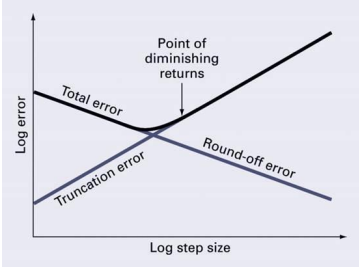
(3) Total Numerical Error
총 Numerical error는 truncation error, roundoff error의 합이다. 스텝 크기가 증가할 때 [1] truncation error는 같이 증가하고, [2] roundoff error는 감소하므로 스텝 크기에 대한 수익이 감소한다.
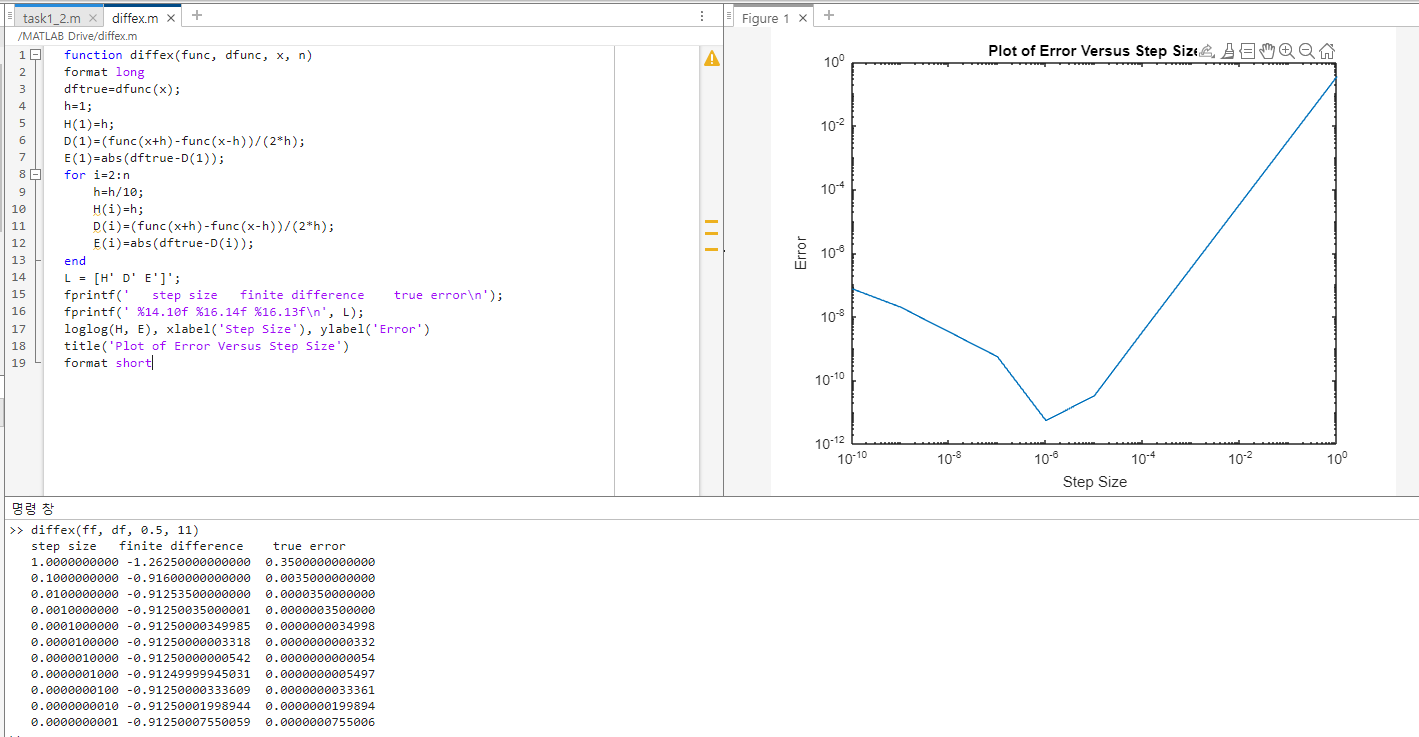
예제를 풀어보겠다. f(x) = -0.1x^4-0.15x^3-0.5x^2-0.25x+1.2이다. centered difference approximation을 이용하여 x = 0.5에서의 첫번째 도함수를 추정하자.
#% 4개의 입력 인수를 받는다.
#% 주어진 함수 'func'의 도함수 'dfunc'을 사용하여 근사화하고, 그 과정을 'n'단계 수행.
function diffex(func, dfunc, x, n)
#% 출력 형식을 긴 형식으로 설정한다.
format long
#% 주어진 위치 'x'에서의 실제 도함수 값
dftrue=dfunc(x);
#% 스텝 크기 'h'를 설정하고, 3개의 배열을 초기화한다.
h=1;
H(1)=h;
D(1)=(func(x+h)-func(x-h))/(2*h);
E(1)=abs(dftrue-D(1));
for i=2:n
h=h/10;
H(i)=h;
D(i)=(func(x+h)-func(x-h))/(2*h);
E(i)=abs(dftrue-D(i));
end
#% H, D, E 배열을 열 벡터로 변환하고, 이들을 행렬 'L'에 저장한다.
L = [H' D' E']';
#% 결과를 화면에 출력한다.
fprintf(' step size finite difference true error\n');
fprintf(' %14.10f %16.14f %16.13f\n', L);
#% 오차와 스텝 크기 간의 관계를 로그-로그 스케일로 그래프로 표시한다.
loglog(H, E), xlabel('Step Size'), ylabel('Error')
title('Plot of Error Versus Step Size')
format short
그래서 이러한 지점 간의 tradeoff가 매우 중요하다. optimal step size 공식은 아래와 같다.
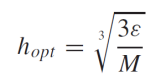
'KNU_study > 수치해석' 카테고리의 다른 글
| 수치해석(7) Linear Algebraic Equations and Matrices (0) | 2023.11.01 |
|---|---|
| 수치해석(5) Roots: Open Methods (1) | 2023.10.31 |
| 수치해석(4) Roots: Bracketing Methods (0) | 2023.10.31 |
| 수치해석(2) MATLAB 실습 (2) | 2023.10.28 |
| 수치해석(1) Mathmatical Modeling, Numerical Methods and Problem Solving (0) | 2023.10.27 |



