1. Curve fitting
데이터는 discrete value(이산값)으로 보통 주어진다. 그런데, 이산값 사이의 점에서 estimates(추정치)가 필요하다. 또한 복잡한 기능의 단순화된 버전이 필요하다. 이러한 응용은 Curve fitting에 의해 수행된다.
Curve fitting에 대한 2가지 일반적인 접근법이 존재한다. [1] 데이터가 상당한 오차를 가지는, 데이터의 일반적인 추세를 나타내는 단일 곡선을 도출하는 것이다. [2] 데이터를 매우 정확히 사용하여 각 점을 직접 통과하는 곡선 또는 일련의 곡선을 맞춘다. 아래 그림으로 이해하자.

2. Linear Regression
Curve fitting의 간단한 번지점프 예시를 들어보자. 번지점프와 같이 자유낙하하는 물체는 공기저항의 상승력을 받는다. 아래 공식과 같이 이 힘은 속도의 제곱에 비례한다.

어떻게 하면, force versus velocity 데이터와 맞는 최고의 선 또는 곡선을 그릴까?
(1) Statistics Review
[1] Measure of Location를 알아보자. Arithmetic mean은 산술적인 방법으로 평균을 구하는 것으로, 각각의 데이터를 더한 값을 데이터의 개수에 나누어 구한다. Median은 데이터 그룹의 중앙값이며, Mode는 데이터 그룹에서 가장 많이 발생하는 값이다.
[2] Measure of Spread를 알아보자. Standard deviation은 표준편차로, 아래와 같이 구한다. 이때 (n-1)의 값을 자유도라고 한다. Variance는 분산이며, 공분산인 Coefficient of variation의 공식은 아래와 같다.

(2) MATLAB commands
### Dexcriptive Statistics, Histograms in MATLAB ###
#% 참고로 행렬이 주어지면, 각 열에 대해 통계량이 반환된다.
mean(s), median(s), mode(s)
#% Calculate the mean, median, and mode of s.
#% mode is a part of the statistics toolbox.
min(s), max(s)
#% Calculate the minimum and maximum value in s.
var(s), std(s)
#% Calculate the variance and standard deviation of s
[n,x] = hist(s,x)
#% s의 각 data bin에 포함된 요소의 수를 결정.
#% x는 bin의 중심값을 나타내는 벡터다.
[n,x] = hist(s, m)
#% m개의 bin을 사용하여 s개의 data bin에 포함된 요소의 수를 결정.
#% x는 bin의 중심값을 나타내는 벡터이고, 디폴트로 m = 10이다.
hist(s,x) or hist(s,m) or hist(s)
#% 이처럼 출력 인수가 없다면, 실제로 히스토그램이 생성된다.

### Random numbers in MATLAB ###
r = rand(m, n)
#% 0과 1 사이에 균일하게 분포된 수열을 생성한다.
#% r은 m x n 행렬의 난수다.
runiform = low + (up – low) * rand(m, n)
#% 다른 구간에서도 균일한 분포를 사용할 수 있는 공식.
r = randn(m, n)
#% 평균이 0이고, 표준편차가 1인 정규 분포를 따르는 일련의 숫자 생성.
#% r은 m x n 행렬의 난수다.
rnormal = mn + s * randn(m, n)
#% 이 공식을 사용하면, 다른 평균 값(mn)과 표준 편차값(s)을 갖는 정규 분포 생성 가능.
(3) Linear Least-Squares Regression (Fitting)
선형 최소 제곱 회귀 분석은 주어진 데이터 집합에 대한 선형 모형에서 '최상의' 계수를 결정하는 방법이다. '최상'이 되려면, 적합 모형과 데이터 점(xi, yi) 사이의 e를 최소화하면 된다. e는 error 또는 residual이라고 한다. 아래 그림을 보면, 아주 이해가 잘 될 것이다.
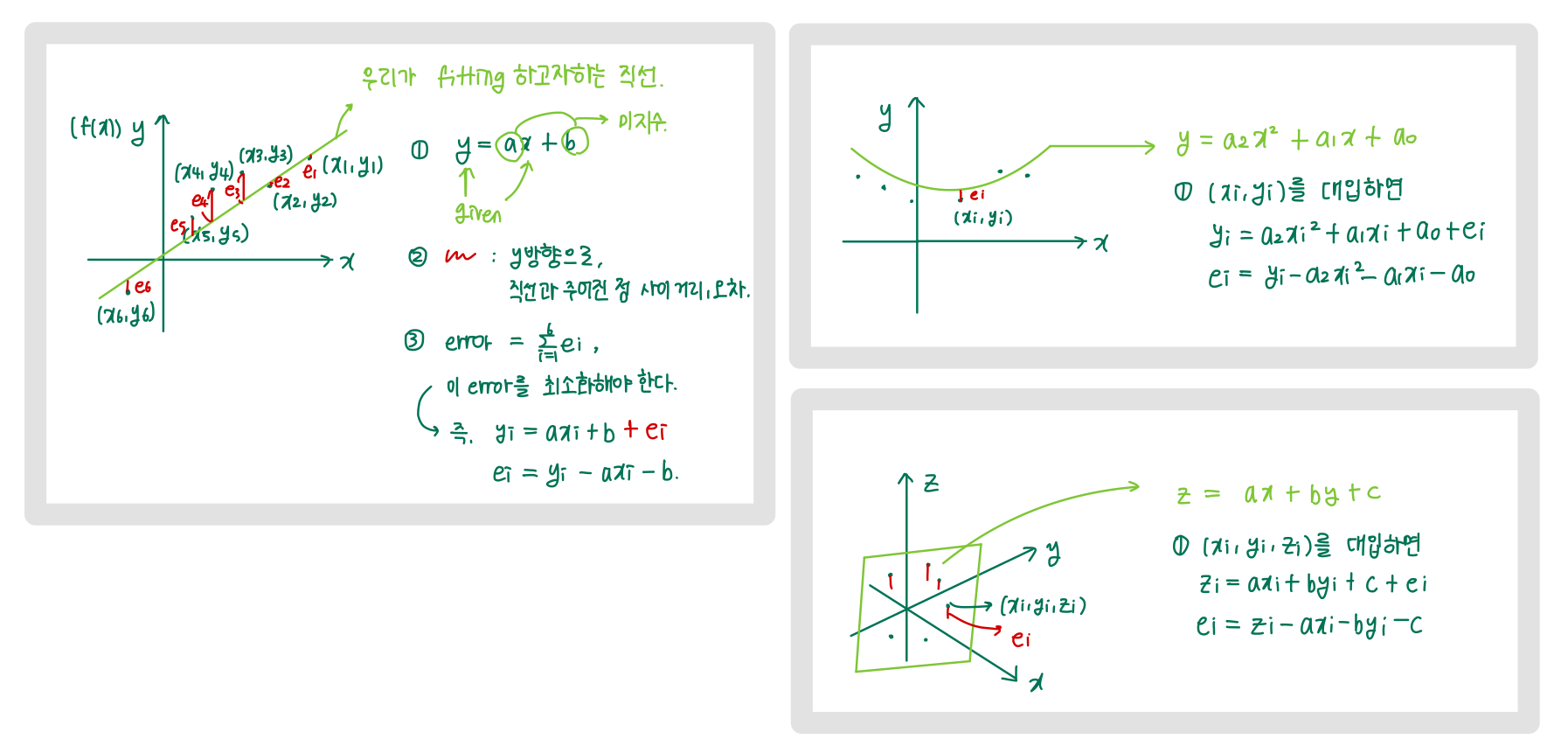
추가적으로, e1 = 5이고 e2 = -5인 경우에 error의 sum을 구하면 상쇄될 수 있다. e2 공식을 사용하자.

또한 아래의 모델에서, 우리가 구해야 하는 것은 a0와 a1이므로, 다음 공식을 통해 구하자. 즉 fitting하려는 function과의 오차들의 합이 최소화되어야 하므로, 최소화를 미지수에 대한 편미분 = 0으로 두고 수행한다.



coefficient of determination r2은 fitting이 잘 되었는지를 나타내는 값으로, model에서 설명하는 원래 불확실성의 백분율을 나타낸다. 일반적으로 r2가 1일 때, Sr가 0일 때 좋은 fitting이라 한다. r2 = 0이라면, 단순히 평균을 선택하는 것보다 개선이 없다. 또한 r2 < 0인 경우, model은 단순히 평균을 선택하는 것보다 더 좋지 않다.

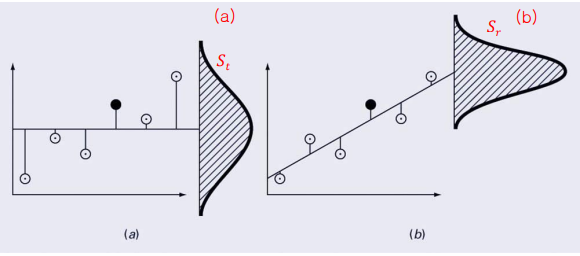
r2가 1에 가깝다고 해서 적합도가 반드시 '좋음'을 의미하진 않는다. 아래 경우들을 참고하자.

예제 14.4와 14.5는 꼭 풀고 넘어가자.
(4) MATLAB Functions
p = polyfit(x, y, n)
#% this function fits a least-squeares nth order polynomial to data.
#% x : 독립변수, y : 종속 변수
#% n : 다항식의 차수(order)
#% p : 다항식의 계수(coefficients)
(5) Multiple linear regression

선형 회귀 분석의 또다른 유용한 확장은 윗 그림처럼 y가 2개 이상 독립 변수의 선형 함수인 경우다. 역시, 추정 오차의 제곱의 합을 최소화하여 best fit을 구한다.


예를 들어, t가 2개의 독립 변수로 이루어졌다고 가정해보자. 계수들의 best value는 아래 Sr에 의해 결정된다. 또한 각각의 계수로 미분한 것은 아래 식과 같다.
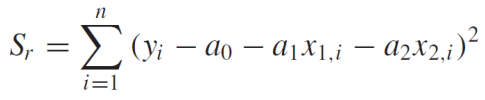

오차 제곱의 최소 합을 산출하는 계수를 편미분을 0으로 설정하고, 결과를 행렬 형태로 표현하면 다음과 같다.

(6) General Linear Least Squares
다중 선형 회귀 분석은 일반 선형 최소 제곱 모델에 속한다.

식은 matrix equation으로 표현될 수 있다.


{y}는 종속 데이터, {a}는 방정식의 계수를 포함하고, {e}는 각 지점의 오류를 포함하고, [Z]는 아래와 같다. z ij는 i번째에서 계산된 j번째 기저 함수의 값을 의미한다.
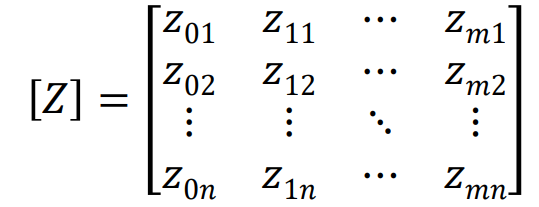
일반적으로 [Z]는 정방 행렬이 아니어서, {a}를 구하기 위한 간단한 inversion이 불가능하다. 대신 양변에, [Z]의 전치 행렬을 곱해주면 정방 행렬로 바뀌게 되어 {a}를 구하기 위한 간단한 inversion이 가능해진다.

3. NonLinear Regression
(1) chapter 14의 방법
선형 회귀 분석은 종속 변수와 독립 변수 사이의 관계가 선형이라는 사실에 기초한다. 예외적인 Nonlinear Relationships일 경우, 아래 표처럼 비선형 식들은 Linearized(선형화)하여 문제를 푼다.
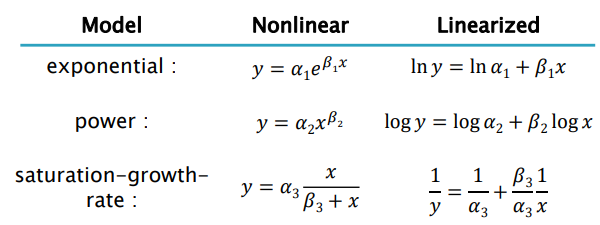

(2) Polynomial Regression
추정 오차의 제곱의 합을 최소화하자. 고차 다항식을 사용하면 더 복잡한 데이터 패턴을 모델링할 수 있다.

m차 다항식의 오차 제곱의 합은 아래와 같으며, 이를 최소화하는 것이 best fit이다.



(3) MATLAB Functions
공학 및 과학 분야에서는 비선형 모델이 데이터에 적합해야 하는 경우가 많다. 아래와 같은 식을 보자.

완벽한 nonlinear regression을 위한 한가지 방법은 least-squares fit을 직접적으로 결정하는 것이다.

MATLAB에서 비선형 회귀 분석을 수행하려면 fit에 대한 추정 오차의 제곱의 합을 반환하는 함수를 작성한 다음, fminsearch 함수를 사용하여 최소값이 발생하는 계수 값을 찾는다. Sr을 계산하는 함수의 인수는 계수, 독립 변수 및 종속 변수여야 한다. 아래 식을 위한 코드는 다음과 같다.

#% FSSR.m 함수
function f = fSSR(a, xm, ym)
yp = a(1)*xm.^a(2);
f = sum((ym-yp).^2);
#% command window
a = fminsearch(@fSSR, [1, 1], [], v, F)
#% [1, 1] : initial guess for the [a0, a1]
#% [] : a placeholder for the options
결과 계수는 data에 대해 가장 큰 r2를 생성하며, 변환에 의해 생성된 계수와 다를 수 있다.
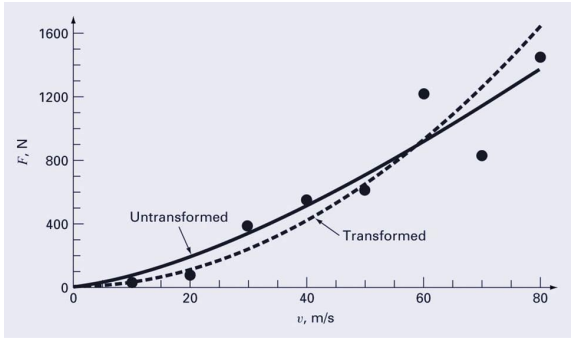
(4) Nonlinear least-square fitting
Least-square fitting은 오차의 제곱의 합을 최소화하는 방법이다. 이때까지 계속 했던 것.
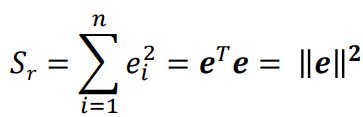

비선형 함수의 minimum 찾는 방법을 비선형 데이터 fitting에도 적용할 수 있다. 다양한 비선형 최적화 방법 중 하나인 Gauss-Newton 방법으로 구해보자. 왜냐면, Sr = ||ek||2를 최소화 한다는 것은 S의 미분이 0인 x의 값을 찾는다는 의미다. S' = 2||e(xk)||e(xk) = 0이므로 e(xk) = 0을 구하는 것과 동일하다.
n개의 비선형 함수, n개의 미지수에 대한 비선형 시스템의 solution은 아래 공식을 사용한다.

m개의 비선형 (오차) 함수, n개의 미지수가 있을 때는 아래 공식을 사용한다. (m>n)

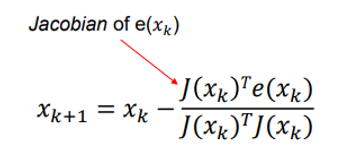
간단한 예시를 들어보자. 아래와 같은 식이 있다.


e(x)는 다음과 같이 표현할 수 있다. 참고로, e = f(t) - y 혹은 e = y - f(t) 모두 가능하다.
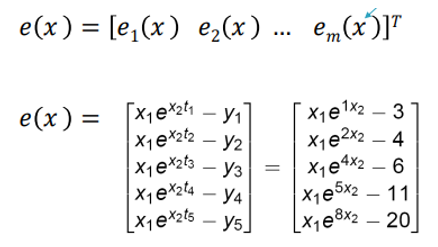
자코비안 행렬 역시, 다음과 같이 x1과 x2에 대해 미분한 요소들로 구성된 행렬로 표현된다.

해당 예제에서 구하려는 벡터는 x = (x1, x2)' 이므로 iteration (k)에서 값을 구할 수 있으며, 수렴할 때까지 과정을 수행하면 된다.
(5) Nonlinear least-square fitting code
코드는 아래와 같다.
function a = GaussNewton(x,y)
tol = 0.0001; % tolerance
a = [2,3]; % initial value
iter_max = 50; % max iteration
n = length(x); % number of data point
disp('ietration a0 a1 da0 da1');
for iter = 1:iter_max
a0 = a(1);
a1 = a(2);
for i = 1:n
f(i) = exp(-a0*x(i)).*cos(a1*x(i));
j(i,1) = -x(i).*exp(-a0*x(i)).*cos(a1*x(i));
j(i,2) = -x(i).*exp(-a0*x(i)).*sin(a1*x(i));
d(i) =y(i)-f(i);
end
da = (j'*j)\(j'*d');
a =a + da';
out = [iter a da'];
disp(out);
if(abs(da(1)) < tol && abs(da(2)) < tol)
disp('Gauss-Newton method has converged.');
break
end
end
x1 = min(x);
x2 = max(x);
xx = linspace(x1,x2,100);
yy = exp(-a0*xx).*cos(a1*xx);
plot(xx,yy,x,y,'ro');
'KNU_study > 수치해석' 카테고리의 다른 글
| 수치해석(14) Splines and Piecewise Interpolation (0) | 2023.12.25 |
|---|---|
| 수치해석(13) Polynomial Interpolation (1) | 2023.12.23 |
| 수치해석(11) Eigenvalue (1) | 2023.12.23 |
| 수치해석(10) Iterative Method(To solve linear system and non-linear system) (1) | 2023.12.23 |
| 수치해석(9) Matrix Inverse and Condition (0) | 2023.12.23 |



