interpolation, 보간법이란 이산적으로 띄엄띄엄 주어진 데이터들을 적절한 곡선으로 이어서, 주어지지 않은 데이터 값을 가상으로 만들어주는 작업이다. 주어진 데이터를 모두 지나는 '근사 함수'를 구한다고 보자.

1. Polynomial Interpolation
(1) Polynomial interpolation
정확한 데이터 지점 간의 중간 값을 추정하는 경우가 자주 발생한다. interpolate(보간)에 사용하는 함수는 실제 데이터 점을 통과해야 하므로 interpolation은 fitting보다 좀 더 제한적인 알고리즘이다. 가장 일반적인 방법은 n개의 데이터 포인트를 통과하는 (n-1)차 다항식을 해결하는 방법이다.


Polynomial interpolation(다항식 보간)은 데이터 포인트 n만큼의 기저 함수를 제공하므로, 선형 대수를 사용하여 다항식 계수를 정확하게 구할 수 있다. 또한 matlab의 polyfit 명령어, polyval 명령어도 사용할 수 있으며 n개의 데이터 포인트에 대한 fit 순서가 (n-1)인지 확인하기만 하면 된다.

(2) Polynomial interpolation problems
다항식의 계수를 푸는 과정에서의 한 가지 문제는, invert되는 시스템의 형태가 아래와 같다는 것이다.

왼쪽의 행렬은 Vandermonde matrices로 알려져 있으며, round-off error(반올림 오차)에 매우 민감하다. 이러한 문제는 데이터를 확장 및 이동함으로써 최소화할 수 있다. interpolation에선 미지수 개수 = equation 개수이므로 Ax = b의 식에서 A를 바로 inverse취하면 된다. 따라서 이 문제가 별로 문제되진 않지만, 참고 사진은 아래에 첨부하였다.


(3) Polynomial interpolation code
MATLAB의 polyfit, polyval function을 사용하면 다음과 같다.
format long
T = [300 400 500];
density = [0.616 0.525 0.457];
p = polyfit(T, density, 2);
d = polyval(p, 350)
2. Newton Interpolating Polynomials
polynomial interpolation을 수행하면 반올림 오류가 발생할 수 있다. 이를 해결하기 위한 방법에는 Newton과 Lagrange의 방법이 존재한다.
(1) Newton interpolating polynomials

위의 사진은 단순 다항식과 뉴턴의 1차 보간 다항식을 비교한 것이다.
first-order Newton interpolating formula(1차 뉴턴 보간 다항식)은 아래 그림과 같이 선형 보간 및 유사 삼각형에서 얻을 수 있다. 알려진 점인 x1과 x2를 기반으로 한 결과는 다음과 같다.

1차 뉴턴 보간 다항식은 직선으로 곡선을 근사하는 방식으로, 오류가 클 수 있다. 추정치를 개선하기 위한 방법은 점들을 연결하는 선에 곡률을 도입하는 것이다. 3개의 데이터 점이 사용가능한 경우, second-order Newton interpolating polynomial(2차 뉴턴 보간 다항식)을 사용할 수 있다. 알려진 점 x1, x2, x3을 기반으로 한 결과는 다음과 같다.

(2) Newton interpolating polynomials - general form
앞의 분석들은 (n-1)차 다항식에서 n개의 데이터 점에 적합하도록 일반화할 수 있다.

이때 f는 divided differences를 나타내는데, 이는 아래와 같이 구해진다. 이는 이전 하위 차수의 차이를 사용하여 계산된다.

3. Lagrange Interpolating Polynomials
(1) Lagrange interpolating polynomials
이동된 값을 사용하여 보간 다항식을 표현하는 또다른 방법이다.
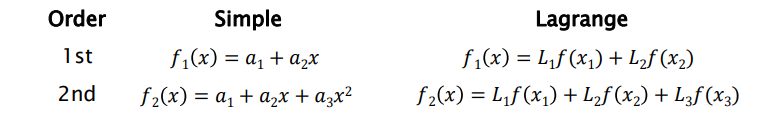
위의 사진은 단순 다항식과 라그랑주 보간 다항식을 비교한 것이다.
first-order Lagrange interpolating polynomial(1차 라그랑주 보간 다항식)은 2개의 선형 보간들의 가중 조합으로부터 얻을 수 있다. 알려진 점 x1, x2를 기반으로 한 결과는 다음과 같다.
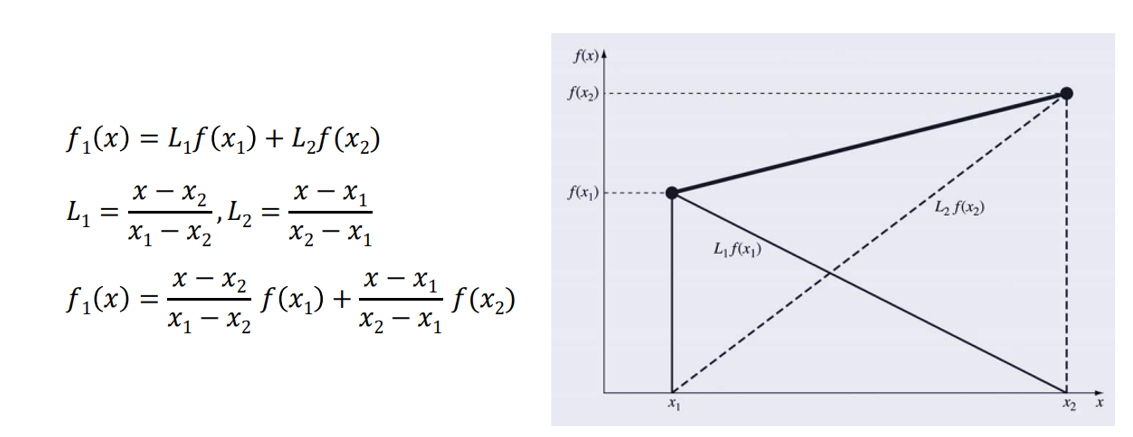
second-order Lagrange interpolation polynomial(2차 라그랑주 보간 다항식)은 아래와 같다.

(2) Lagrange interpolating polynomials - general form
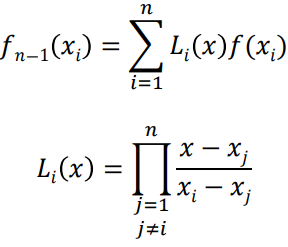
(3) Extrapolation
Extrapolation은 알려진 기본 점 x1, x2, ... , xn의 범위 밖에 있는 f(x)의 값을 추정하는 과정이다. 미지의 영역으로 들어가는 단계를 나타내며, 주의가 필요한 과정이다.

(4) Oscillations
고차 다항식 보간의 위험이다. 예제 17.7을 참고하자.

예제 17. 1-4 꼭 풀자.
TMI

'KNU_study > 수치해석' 카테고리의 다른 글
| 수치해석(14) Splines and Piecewise Interpolation (0) | 2023.12.25 |
|---|---|
| 수치해석(12) Linear Regression (1) | 2023.12.23 |
| 수치해석(11) Eigenvalue (1) | 2023.12.23 |
| 수치해석(10) Iterative Method(To solve linear system and non-linear system) (1) | 2023.12.23 |
| 수치해석(9) Matrix Inverse and Condition (0) | 2023.12.23 |



