Linearization
** 근의 위치가 파라미터에 따라서 바뀐다 (매트랩 하기) 비선형일 경우, 시뮬레이션은 여전히 가능하다.

그러나 비선형 함수의 라플라스 변환은 불가능하다
비선형 함수를 선형화해야지 라플라스 변환 등을 활용할 수 있다.

선형화한다는 것은 [동작점]을 필요로 한다.
-> 주로 동작점(operating point)을 x0로 둔다.
-> 선형화 = 동작점에서의 직선을 찾는 것
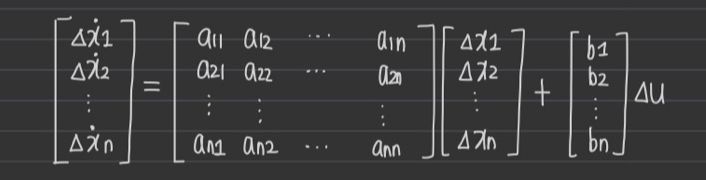
비선형 방정식은 주로 고차 미분방정식으로 나타내어진다.
이를 상태미분방정식으로 바꾸면 일차 미분 방정식 n개로 나타내어진다.

비선형일 경우의 dynamic equation과 동작점은 아래 식과 같다.

선형시스템의 동작점은 항상 0이다.
그러나 비선형 시스템의 동작점은 ,, 무수히 많이 존재할 수 있다.
** 동작점, 정상 상태가 되었을 때 움직이지 않는, 즉 상태방정식의 좌항(미분)이 0이 되는 점.
-> nonlinear dynamic equation을 풀어서 미분이 0 되는 지점을 찾자.
Linearization process
(1) suppose

(2) 동작점에 대해서 테일러시리즈로 전개한다.

(3) 편미분을 해서 선형 미분방정식을 얻는다.
** 편미분이 힘든, 복잡한 식은 매트랩 툴을 이용하면 된다.
(4) linearization model
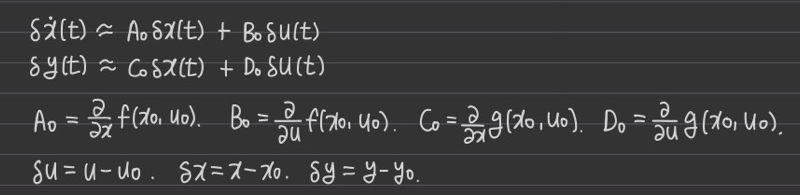

이렇게 비선형 모델에 선형화된 제어기를 설계하고 적용시킨다.
-> u0를 입력으로 넣어줘야지 (동작점이) 원하는 위치로 가게 된다.
-> 왼쪽 그림이 비선형 제어 [대학원 과정]
예제1

예제2(펜듈럼)

그림11 : 각각 편미분한 값(설명에 추가)
그림12 : 라플라스 변환을 통해 얻은 해(설명)
Performance
Standard performance measure
dynamics가 존재하기 때문에 reference(목표지점)로 바로 갈 순 없다. 서서히 증가하며 도달한다.


-> tp, tr, ts, P.O, s.s.e 등을 알아두자.
Rise time : 10%에서 90%까지 가는 데 걸리는 시간
Settling time : 원래 값의 오차 2% 안에 들어가는 시간
시정수[time constant] : 목표지점의 63%까지 가는 데 걸리는 시간
-> 입력으로 쓰는 신호는 보통 unit-step[u(t)], ramp[r(t)], parabolic(force controll) function 3가지다.
시정수(time constant)

time constant : step response for the general first-order system
-> 즉, 시정수 : 시스템의 응답의 빠르기를 나타내는 값
시정수가 작을수록 빠른 응답을 의미.
시정수가 크다 = 시간이 오래 걸린다 = 속도에 대한 오차가 계속 증가한다
** rising time : 2.2/a, settling time : 4/a
<Two types of response>
Transient response : the response that disappears with time
Steady-state response : the response that exists a long time following any input signal initiation.
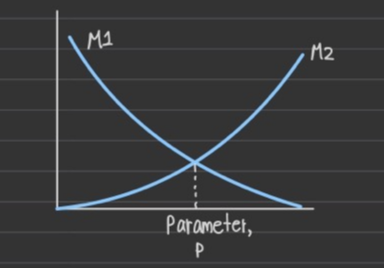
performance에서 목표가 2가지(빠르게 가는 것, energy 줄이는 것)일 때
이 둘을 절충하여, 만족하는 parameter point를 찾아야 한다.
예제1(first-order system, the step input signal)

예제2(second-order system, the step input signal)
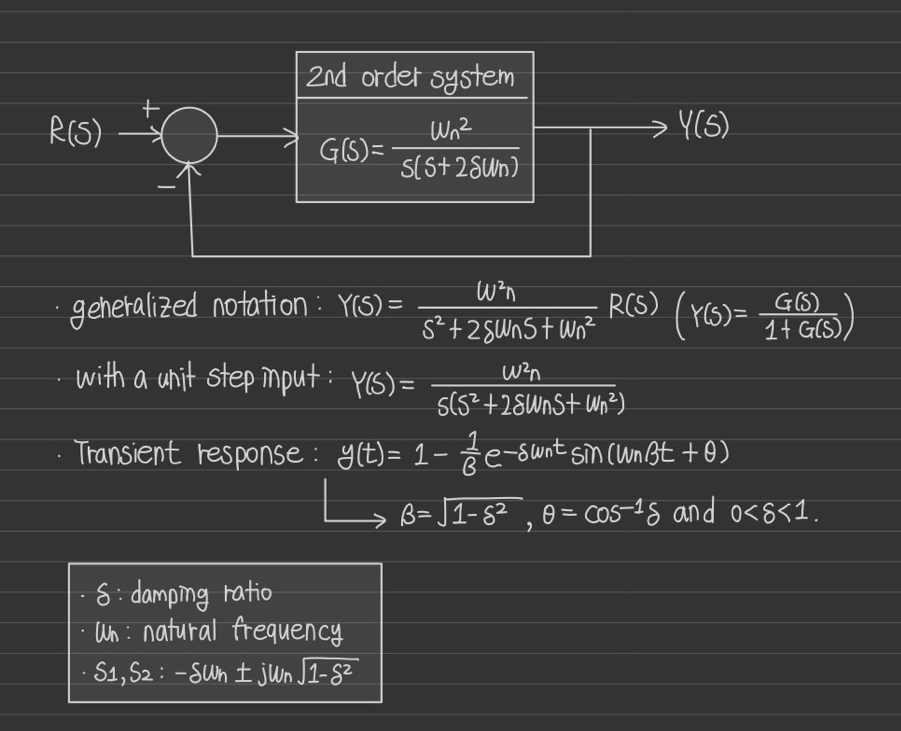
Standard performance measure 공식
** the rise time and the peak time are used to measure the swiftness of the response.
** rise time은 underdamped에서는 0-100%까지의 도달시간, overdamped에서는 10-90%까지의 도달시간을 의미

Settling time(Ts)
-> time required for the system to settle within a certain percentage 세타 of the input amplitude.
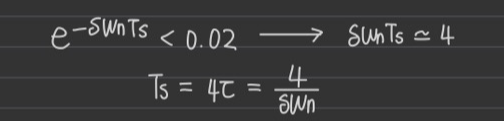
Overshoot and peak time versus damping ratio

하나씩 자세히 유도해보자.




상승 시간은 고유 진동수에 반비례
최대 초과는 감쇠비에 의해 결정
정착 시간은 극점의 실수부에 반비례
** damping ratio는 0.5, 0.6, 0.7을 많이 사용한다.
'LAB > 제어이론' 카테고리의 다른 글
| 제어 이론(10) 관측기[Observer] (2) | 2023.08.09 |
|---|---|
| 자동제어 : 매트랩 실습 (0) | 2023.04.26 |
| 자동제어(4-2) disturbance, noise, steady-state error (0) | 2023.01.31 |
| 자동제어(4) feedback control, error signal analysis, sensitivity (0) | 2023.01.30 |
| 자동제어(3-3) state-space equation (0) | 2023.01.30 |



