모델
1. ordinary differential equation -> Laplace transform -> transform function
2. signal flow [전달함수를 좀 더 쉽게 구하기 위해서]
3. 상태 방정식
State space equation
수학에서 space란, 집합으로 생각하면 된다.
즉, '상태'라는 집합을 정의해서 거기다가 equation을 해석한다.
전달함수 형태의 미분 방정식 -> 시간 영역에서 풀어보자.
움직이는 물체를 다룬다. -> 움직이는 물체는 미분 방정식으로 표현된다. ->
시간 영역이 다루기 어렵기에 라플라스 변환(주파수 영역)으로 풀곤 했다. -> 컴퓨터 연산은 시간 영역에서 가능.
** 비선형은 라플라스 변환이 불가능. -> time domain이 용이할 때가 많다.
** 고차 미분방정식은 시간으로 어떻게 표현하는가

dynamic system : 미분 방정식으로 표현되는 상태들의 결합
x(t) : dynamic system의 상태 변수, [초기 조건]과 [input]에 영향을 받는다.
-> x(t)가 배열로 표현되는데, 그 중에 관심있는 부분을 출력으로 뽑아낸다.
예제 : A spring-mass-damper system

2차 미분 방정식 형태로 표현된다.
위치, 속도를 각각 x1, x2로 잡고 상태 방정식을 푼다.
예제 : RLC 회로

** 전압이 시간에 대해서 변할 때 전류가 흐른다.
** 출력 : Vo, 즉 R에 걸리는 전압
State differential equation

x : state vector, state가 모여진 배열이다. 각 상태를 배열로 표현한 vector.

** simple하게 u=0으로 두면, [단순한 곱셈]의 법칙이 성립함을 알 수 있다.
즉 transition matrix를 가지고 vector 연산을 시행하면 해를 찾을 수 있다. (=상태 방정식의 해의 의미)
** system에서 상태를 정할 때, 한 개의 상태로 고정되어 나오지 않는다.
SFG를 이용하여 상태방정식 찾기
이 미분방정식을 이용하여 SFG를 그릴 수 있다.
(참고로 SFG는 node와 graph로 되어 있다.)
state equation -> signal flow -> 전달함수, 3개의 모델을 등가적으로 구할 수 있다.


또 반대로 전달함수를 가지고 signal flow를 나타낼 수도 있다.
** 일반적으로 상태는 [적분](1/s)으로 표현해야지 전달함수 또는 s의 미분으로 표현하기 쉽다.
Derivation of the signal-flow graph state model

(1) 분모, 분자를 최고차항의 계수로 나눈다.
(2) 4차식이므로 4개의 상태가 있어야 한다. 그러므로 node를 8개 그려두자.

(3) 상태가 8개면 복잡해지니까 4개로 줄여서 사용한다.

A model of dc motor


x1 = y(t) : the velocity output
x2 = i(t) : the field current
x3 = u(t) : the filed voltage

Evaluation of the state transition matrix
(1) 상태 방정식으로 풀기

(2) Signal flow graph model로 풀기
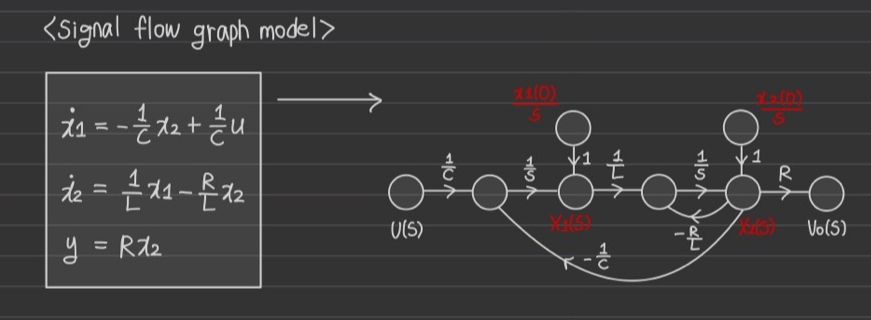
** output과 input은 지워진다.


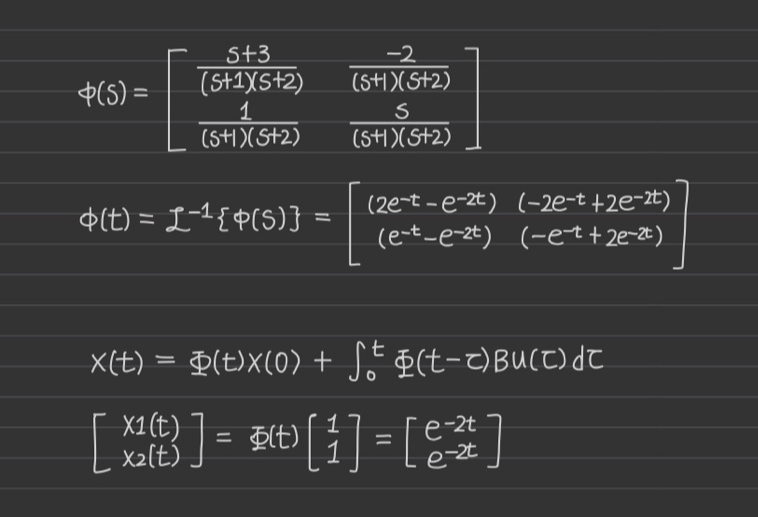
'LAB > 제어이론' 카테고리의 다른 글
| 자동제어(4-2) disturbance, noise, steady-state error (0) | 2023.01.31 |
|---|---|
| 자동제어(4) feedback control, error signal analysis, sensitivity (0) | 2023.01.30 |
| 자동제어(3-2) block diagram, Gain formula(Mason's rule) (0) | 2023.01.30 |
| 자동제어(3) 전달함수 simulation(매트랩) (0) | 2023.01.30 |
| 자동제어(2) mechanical systems, Linearization, laplace transform (0) | 2023.01.30 |



