System/ Control/ Design
1. System
a combination of components acting together to perform a certain objective
입력과 출력 간의 인과관계를 표현한 것
(제어 시스템에서, component = state = 상태로 보면 된다.)
2. Control
Applying inputs to the system to correct or limit deviation of the output values from desired values
3. Design
the process of finding a system that accomplishes a given task
시스템을 만들어가는 일련의 과정
Trial and error
Differential equations of physical systems
for mechanical systems, 뉴턴의 법칙을 따른다.
(관성의 법칙, 가속도의 법칙, 작용 반작용의 법칙)
(어떤 물체에 힘을 가하면 가속도가 변한다.)
for electrical systems, KCL과 KVL을 따른다.
[mechanical systems]
다음 예제를 보자.

질량을 가진 물체에 힘을 가하면, 그 물체는 움직인다.
뉴턴 법칙에 의해 u가 힘이 되고, F = ma를 이용하여 u = m*(dv/vt)를 도출할 수 있다.
그러나, 자동차가 움직일 때 저항하는 힘의 성분이 있을 경우 자동차는 일정한 속도로 움직이게 된다.
그 성분을 속도에 비례하는 저항성분, bv로 둔다.
이를 미분방정식으로 표현한 것이 다음 그림과 같다.

해를 찾는다는 의미는, v(t)를 찾는다는 것이다.
이런 방식으로 2차 미분 방정식도 구할 수 있다.
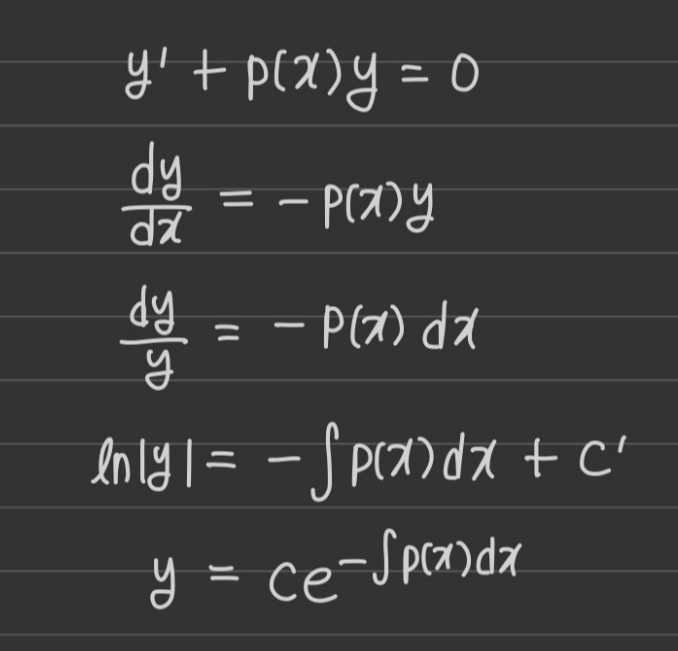
다음 예제를 보자.

어떤 물체에 힘을 주면, 그 결과로 움직이게 될 것이다.
여기서 방해하는 힘은 두 종류가 있다.
스프링에 의해 방해하는 힘(k), 속도에 의해 방해하는 성분(damp, b)이 존재한다.
결론적으로, 질량에 비례해서 가속도가 움직인다. (그것이 뉴턴의 제 2법칙)
또한 이 식을 미분 방적식의 측면에서 보면 2차 미분 방정식이다.
우리는 x(t), 즉 힘을 주고 움직였을 때의 m의 위치를 구하면 된다.
** 각각의 x와 속도(v)를 '상태'라고 말한다.
다음 예제를 보자. (simple spring-mass-damper mechanical system)

움직였을 때 y의 위치, y를 움직일 때의 속도, 외부의 힘에 의한 물리법칙 식 등이 있으면 모델 찾기에 쉽다.
또다른 예제를 보자.

참고로 f(t) 안에 mg(중력가속도)가 들어있다고 보면 된다.
라플라스로 변환된 식을 보면, 분모의 '3'은 c의 값이고, '2'는 k의 값이다.
즉, c와 k의 값에 의해 특성방정식의 근이 결정된다.
그 근 때문에 이 물체의 움직임의 특성이 결정된다.
(+) c=0이 되면, cos 형태의 그래프가 도출된다.
(+) k=0이 되면, 실근(0,3)을 가지므로 exponential하게 줄어든다.
[electrical systems]
아래의 RLC회로에서, 각 노드에서 나가는 전류와 들어오는 전류의 합은 같다.

미분 방정식의 개념에서 2차 미분 방정식을 풀 수 있다.
mechanical에서는 '위치'라는 물리량을 다룬 반면, electrical에서는 '전압'이라는 물리량을 다룰 것이다.
다음 그림을 보자. RLC 회로의 v(t) 그래프 역시 underdamped 형태임을 알 수 있다.

Linear approximations of physical systems
대부분의 자연계는 비선형 시스템이다.
선형(linear)이란 모델을 이용해 예측할 수 있다. 예측이 되니까 제어가 수월하다.
예측이 잘 맞아떨어지려면 덧셈, 곱셈이 잘 지켜지면 된다.

즉, superposition과 homogeneity를 다 만족하면 linear하다.

윗 예시와 같이, 1차식이라고 무조건 linear가 성립하진 않는다.
(+) 적분은 선형을 만족한다. 미분도 선형을 만족한다.
(+) y = ax가 아닌 형태는 거의 다 비선형이다. ex-> y = sinx, y=log x 등
(+) 테일러 시리즈를 이용하여 비선형 식들도 선형으로 나타낼 수 있다.
테일러 시리즈는 비선형 함수를 여러 개 다항식의 합으로 표현할 수 있다.
[Linearization]
선형화 : 비선형 시스템을 선형 시스템으로 바꾸는 과정

동작점에서의 값, 그 점에서의 1차 미분, 그 점에서의 2차 미분 .. 을 이용하여 고차 다항식으로 표현할 수 있다.
즉 y의 변화와, x의 변화의 관계로 식을 나타낼 수 있다. -> 그것이 선형 방정식
** 이 과정에서 중요한 것은 동작점을 찾는 것이다.
동작점에서 테일러 시리즈로 전개하여 1차 다항식만 가지고 표현한 것이 선형화이다. (근사치)
쉬운 예제를 보자.
이차식을 선형화한 값은 다음과 같다.

실제적인 예제를 보자.

penculum 같은 경우, 직선 운동이 아닌 회전 운동을 한다.
(+) 직선 운동에서 일반적으로 힘이 가해지는 것과 달리, 회전 운동에서는 '토크'가 가해진다.

길이가 r일 때, 힘 F를 가해주면 위와 같은 식이 나타난다.
The Laplace transform
라플라스 변환이란?

수학적으로는, 유한한 값을 가지는 것이 중요하다.
1을 0부터 무한대까지 적분하면 무한대가 된다. 이를 수렴하게 하고 싶으면 유한한 값으로 바꿔야한다.
exponential을 곱하면, 수가 유한해진다.

라플라스 : 시간에 있는 신호를 수렴하도록 만들어서 0에서 무한대까지 적분한 것

관련 예제들도 풀어보자.

'LAB > 제어이론' 카테고리의 다른 글
| 자동제어(4) feedback control, error signal analysis, sensitivity (0) | 2023.01.30 |
|---|---|
| 자동제어(3-3) state-space equation (0) | 2023.01.30 |
| 자동제어(3-2) block diagram, Gain formula(Mason's rule) (0) | 2023.01.30 |
| 자동제어(3) 전달함수 simulation(매트랩) (0) | 2023.01.30 |
| 자동제어(1) open loop, closed loop, feedback, future evolution (0) | 2023.01.30 |



