Block diagram models
** system : comference의 결합, 입출력이 여러 개일 수 있다.
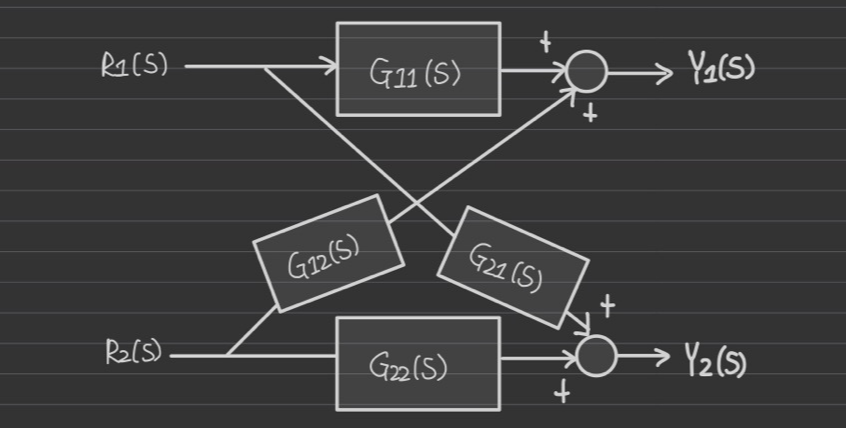

Y1은 n개의 R(s)에 모두 영향을 받아서 출력된다.
이 전체를 [Y=GR]로 표현하게 되면 하나의 전달함수가 되고, G(s)는 하나의 matrix가 된다.
Block diagram Transformations
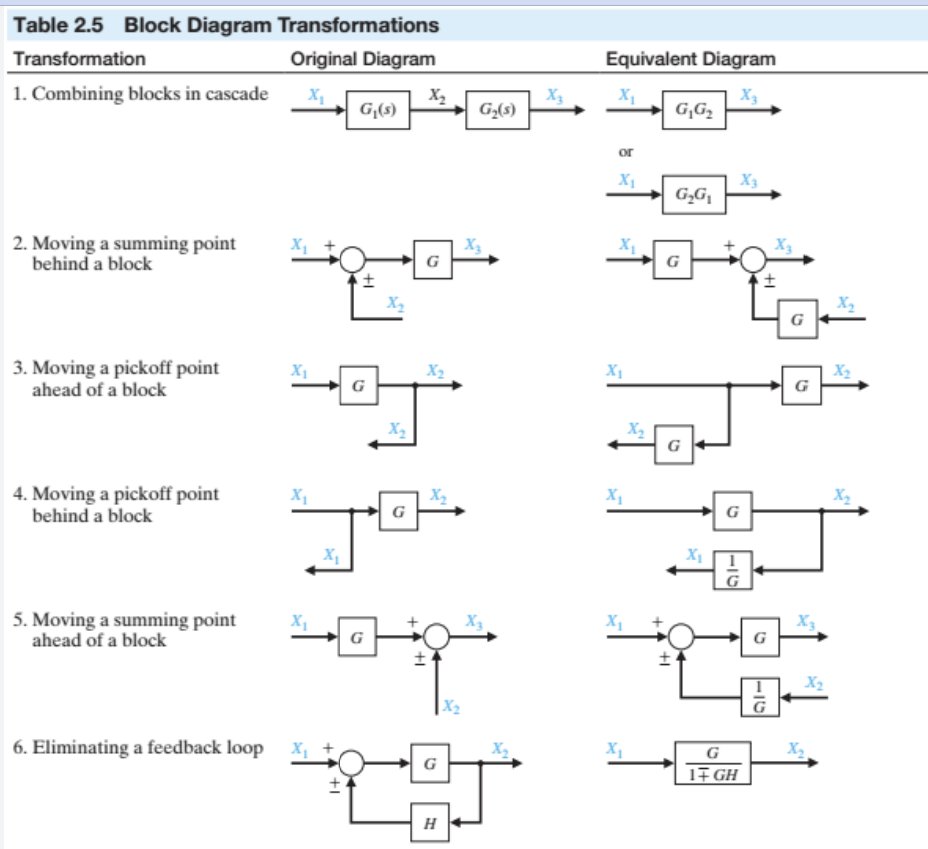
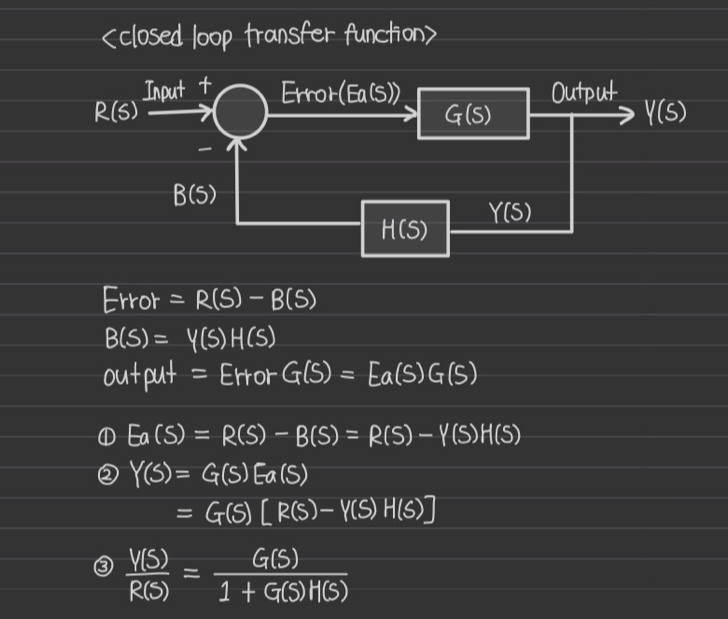
6번을 주목하자. 아래 그림은 Negative feedback control system 증명이다.
분모 : 1 (부호는 original과 반대로) 두 블럭을 곱한값
분자 : path에 있는 블럭
예제
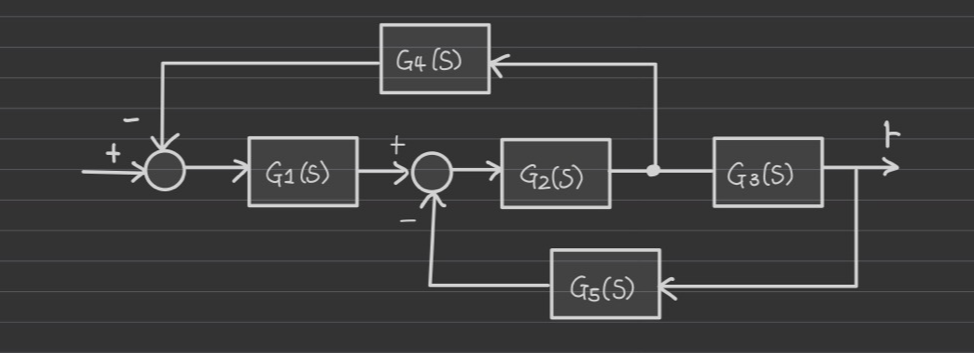
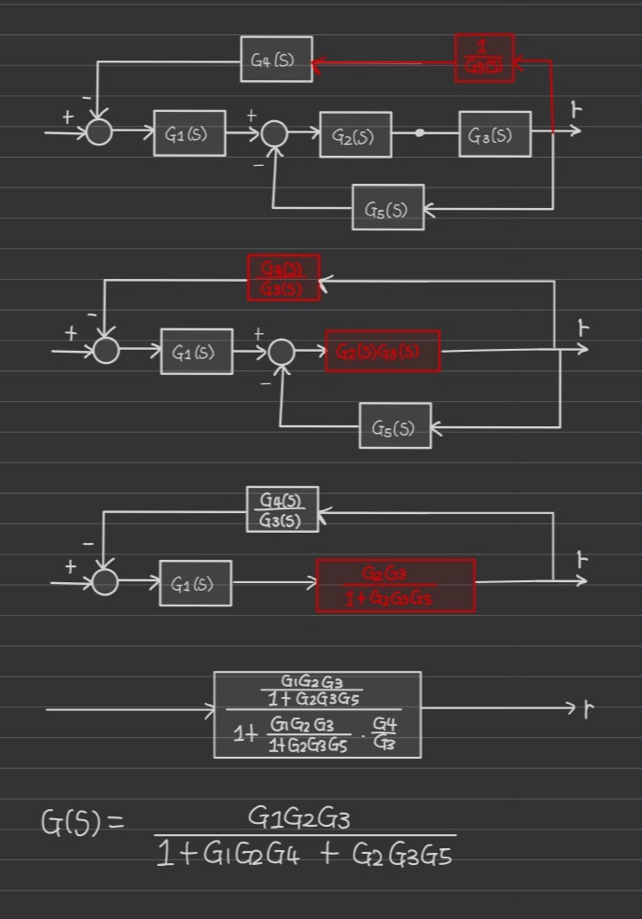
다음 예제는 아래와 같은 순서로 풀면 된다.
(1) moving a pickoff point behind a block (G2 -> G3으로 위치 조정)
(2) combining blocks in cascade(G4와 G3, G2와 G3)
(3) eliminating a feedback loop(loop 2개 다 제거하기)
Signal-flow graph models
블록 다이아그램 전체 system을 하나의 전달함수로 simple하게 나타낼 수 있다.
마찬가지로, 블록 다이아그램 그림을 signal-flow 형태로 표현해보자.
SFG는 node(점, 입출력을 의미), branch(점과 점 사이를 이어줌, 노드 사이에 연결되는 전달함수)로 구성된다.
branch : relates the dependency of an input and an output variables
node : the input and output points or junctions
path : a branch or a continuous sequence of branches that can be traversed from on signal to another
loop : a closed path that originates and terminates on the same node, and along the path no node is met twice
-> 즉, 노드에서 자기 노드로 다시 돌아오는 것.
nontouching : two loops don't have common node
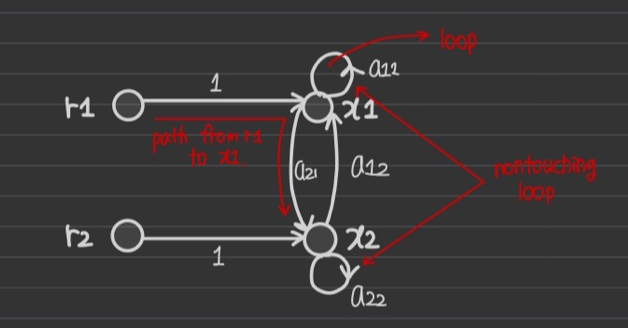
다음 그림에서 입력은 r1, r2이고 출력은 x1, x2이다.
loop는 총 3개가 있다. 맨 위와 맨 아래의 loop 2개는 nontouching loop이다.
Gain formula(Mason's rule)
(1) x1의 결과가 얻어지려면 들어오는 화살표만 생각해보자.
-> x1, x2모두 들어오는 branch는 3개씩 있다. 이를 생각하며 식을 세우면 아래와 같다.
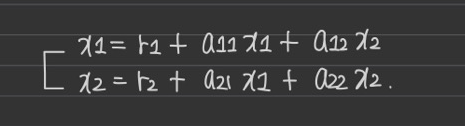
(2) matrix equation으로 풀면 해가 도출된다.

(3) 도출된 해를 보고, 규칙을 찾아보자.
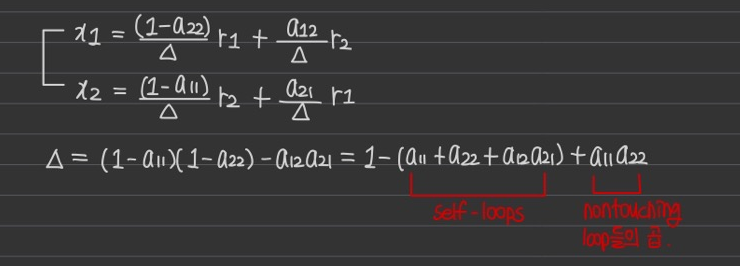
** x1, x2의 분모는 loop와 관련되어 있고, 분자는 path와 관련되어 있다.
** nontouching loop가 여러 개 있으면 [1 - * + ** - ***]처럼 부호를 바꿔가며 식에 넣는다.
Mason's rule 최종 정리
전달함수를 구할 때
분모에 해당하는 부분 : loop에 해당되는 (전체 그래프의) determinant
분자에 해당하는 부분 : path, path의 nontouching에 해당하는그래프의 determinant의 곱
각각의 determinant = 1 - [single loop] + [2개의 nontouching loop] - [3개의 nontouching loop] ...
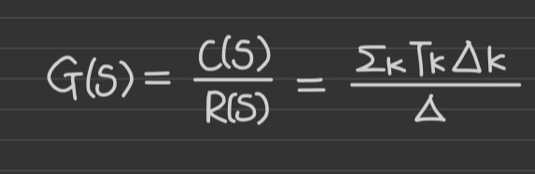
k: forward path gain
Tk: k번째 forward path의 gain
Δ: 1- Σloop gain+ Σ2개 쌍에 대한 nontouching loop gain -Σ 3개 쌍에 대한 nontouching loop gain + Σ4개 쌍에 대한 nontouching loop gain -...
Δk: Δ - Σk번째 forward path를 건드리는 loop gain
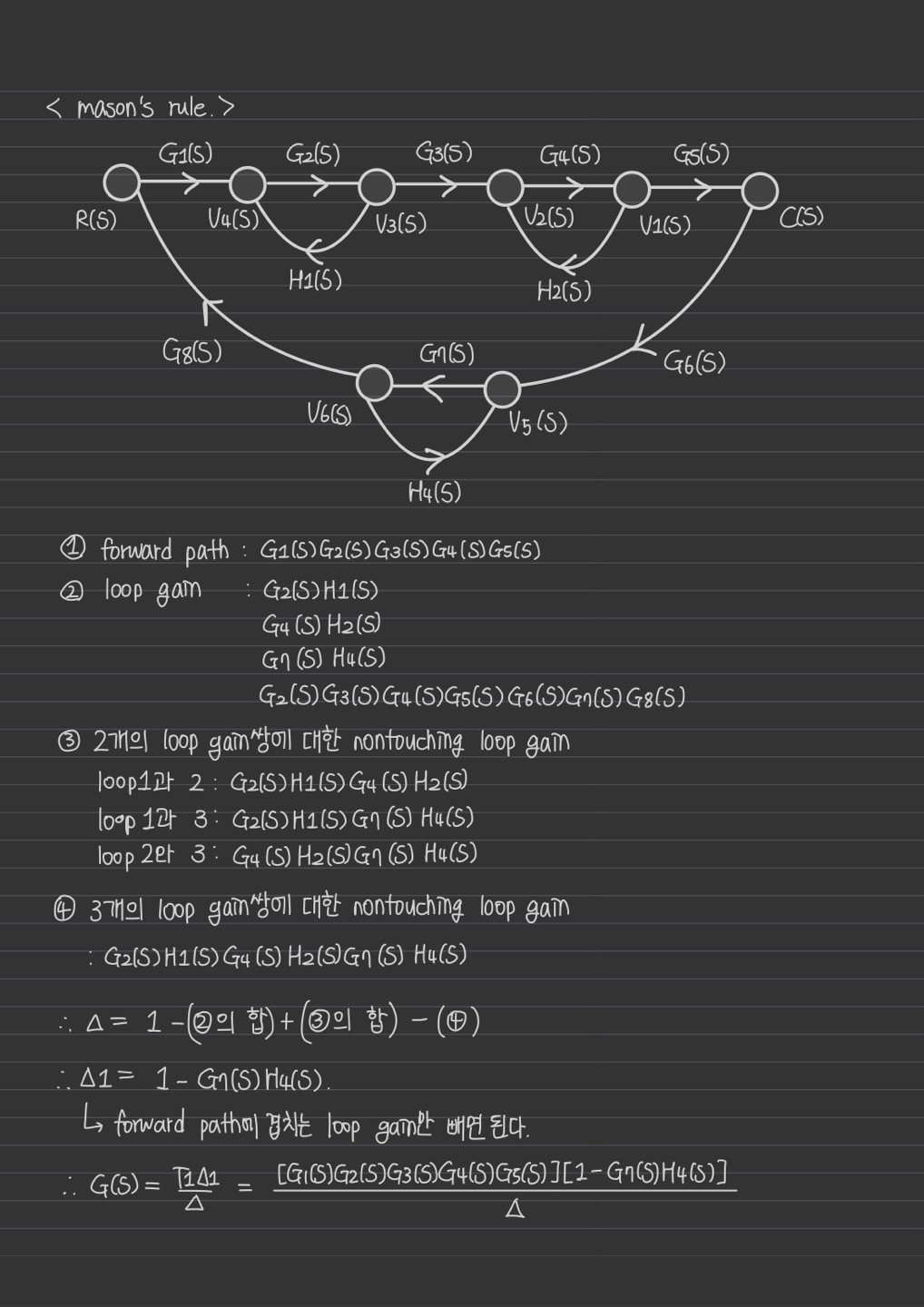
Mason's rule 예제
'LAB > 제어이론' 카테고리의 다른 글
| 자동제어(4) feedback control, error signal analysis, sensitivity (0) | 2023.01.30 |
|---|---|
| 자동제어(3-3) state-space equation (0) | 2023.01.30 |
| 자동제어(3) 전달함수 simulation(매트랩) (0) | 2023.01.30 |
| 자동제어(2) mechanical systems, Linearization, laplace transform (0) | 2023.01.30 |
| 자동제어(1) open loop, closed loop, feedback, future evolution (0) | 2023.01.30 |



