자, 아래에서부터 ddpm에 관한 논문 리뷰가 본격적으로 이루어질 것이다. 그 전에. 신우상 박사님의 세미나를 들은 이후, ddpm에 관해 그리고 생성모델에 관해 깊은 생각을 할 수 있었다. 관련된 생각을 정리해보자.
learning이란? criterion을 가지로 거리를 정의하는 것이다. '우리가 대학교 전공을 얼마나 잘 이해하였는가'는 '대학교 시험 점수'라는 criterion(기준)으로 판단할 수 있다. 이처럼, learning을 할 때에는 기준 그리고 기준과의 거리에 대해 생각할 필요가 있다.
manifold란 고차원 데이터를 저차원에서도 잘 표현하는 공간을 의미한다. 이를 좀 더 비유적으로 설명해보자. 확률과정 과목에서 배웠듯이 continuous space에서 one point의 확률(연속공간에서 한 점의 확률)은 0이다. continuous space = 3차원, one point = [3차원 속의] 2차원 속에 있는 1차원 값으로 둔다면, 3차원에서 1차원의 값들을 뽑을 확률은 0인 것이다. 예시를 들어 보자. 우주와 지구가 있다. 우주에선 지구의 표면에만 사람들이 살고 있다. 여기선 2차원인 지구 표면, 그 위에 있는 사람들을 촥 펼쳐 놓은 지도가 latent space다. 다시 말해 우주에서 사람 한 명을 뽑을 확률은 0이다.
VAE란 무엇일까. VAE란 latent space와 manifold를 mapping하는 샘플링 함수를 찾는 알고리즘이다. 즉, manifold 공간에서 하나의 샘플을 뽑는 것과 동일한 효과를 가진다.
반면 ddpm은 ambient space(전체 공간, 위의 예시로 따지면 우주에 해당)에서 무작위로 샘플링을 한 후, manifold로 매핑시키는 알고리즘이다. 예시를 활용하자면 우주에서 아무 점이나 뽑고, 그 임의의 점을 지구에 서서히 안착시키는 것이다. 즉 navigate를, manifold로 향하는 vector field(score)들을 추정한다. vector field란 vector들의 set, 모든 위치에서 정의되는 set을 의미한다. field(장)란 '위치'에 대한 방향을 뱉어내는 것이라 보면 된다.
-> denoising process에선 항상 vector field가 정해져있다. 그게 바로 score function의 정의다.
-> 베타와 알파가 어디서 나왔는지 : 머신 러닝에서 hyper parameter란 최적화 대상이 아닌, 즉 크게 쓸모없는 variable을 의미한다. 여기서 베타와 알파는 모두 hyper parameter이고, 저자가 설정한 값들로 큰 의미는 없다. random variable인데 다 '가우시안'으로 표현된 것도 저자가 정의한 것으로, 엄청난 규칙이 아니다.
-> 가우시안으로 표현할 경우, 추상적인 것들을 parametrization할 수 있다는 장점을 가진다.
1. ddpm intro
ddpm이란 diffusion model에서 loss term에 대한 변화가 있는 모델이다. text-to-image 생성에 많이 쓰인다. 'Diffusion'이란 확산이다. 물질들이 점차 번지며, 동일한 농도를 가지게 되는 과정이다.
(1) Markov Chain : (t+1) 시점의 확률은 오직 (t)의 시점에만 의 존한다. Markov 성질을 갖는 이산 확률 과정.
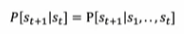
(2) Normalizing Flow : 심층 신경망 기반 확률적 생성 모형 중 하나, 잠재 변수 (Z) 기반 확률적 생성모형.

-> 입력 데이터 샘플 x를 가우시안과 같은 (사전에 정의한 매우 심플한) prior 분포로 매핑하는 함수 f를 학습하도록 한다. 이렇게 학습한 function을 inverse mapping을 통해 prior 분포를 특정한 패턴의 데이터로 생성하는 것.
(3) Overview of generative models
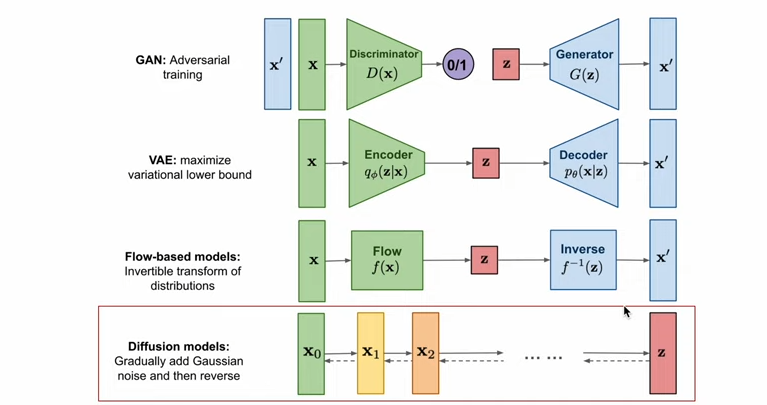
반복적인 변화(iterative transformation)를 활용한다는 점에서 Flow-based models와 유사하다. 분포에 대한 변분적 추론을 통한 학습을 진행한다는 점에서 VAE와 유사하다. 최근에는 Diffusion 모델의 학습에 Adversarial training을 활용하기도 한다.
2. Generative Model overview
(1) Probabilistic Generative model : Latent variable model
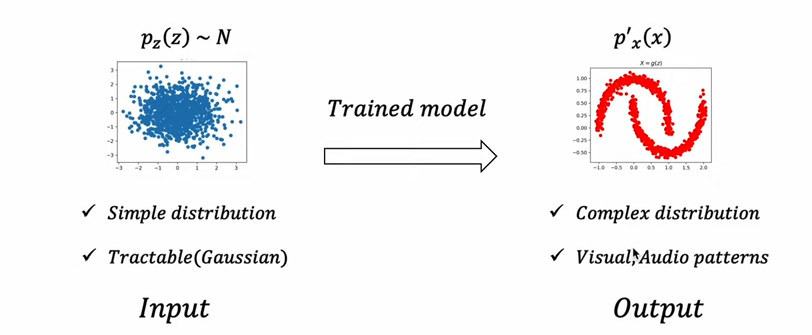
대부분의 생성 모델은 본질적으로 latent variable을 활용한다. 매우 심플한 sample을 input으로 받아서 학습된 모델을 통해 오른쪽과 같은 특정한 패턴의 분포로 변환 혹은 생성한다. 생성모델 과제에서 필요한 것은 [1] input으로 들어갈 latent variable, [2] simple한 것을 complex하게 변화시킬 trained model이다.
결국 생성 모델로부터 원하는 것은 매우 간단한 분포(Z)를 특정한 패턴을 갖는 분포로 변환(mapping)하는 것이다. 대부분 생성모델이 주어진 입력 데이터로부터 latent variable(Z)을 얻어내고, 이를 변환하는 역량을 학습하고자 한다.
(2) VAE
생성과정에서 latent variable을 학습된 decoder를 통해 특정 패턴으로 바꿔낼 수 있다. 이러한 decoder network를 학습시키기 위해 encoder를 같이 학습시킨다. Encoder를 모델 구조에 추가해, Latent variable, Encoder, Decoder를 모두 학습한다. 목표는 likelihood를 극대화하는 것이다.

(3) GAN
심플한 latent variable을 특정한 패턴으로 변화시키고자 하고, 이때 Generator라는 모델이 사용된다. 이러한 Generator를 얻기 위해서, Discriminator network를 추가한다. G와 D가 균형을 찾아가도록 적대적으로 학습을 시킨다.

(4) Flow-based model
이 역시 간단한 분포를 복잡한 패턴으로 변화시키고자 한다. 이러한 과정에서, 학습한 function의 inverse가 활용된다. inverse function의 chain이 'Flow'라고 불리게 되고, Flow가 생성에 활용이 된다. inverse function을 학습하기 위해서 forward 과정을 통해 학습을 수행한다.

(5) Diffusion based generative model
prior를 특정한 패턴으로 변화시키는 모델이 필요하다. 이때의 모델은 특정한 패턴 x를 샘플링할 수 있는 조건부 분포다. 이때 이러한 조건부 분포를 학습시키기 위해 다른 네트워크를 학습시키진 않는다.
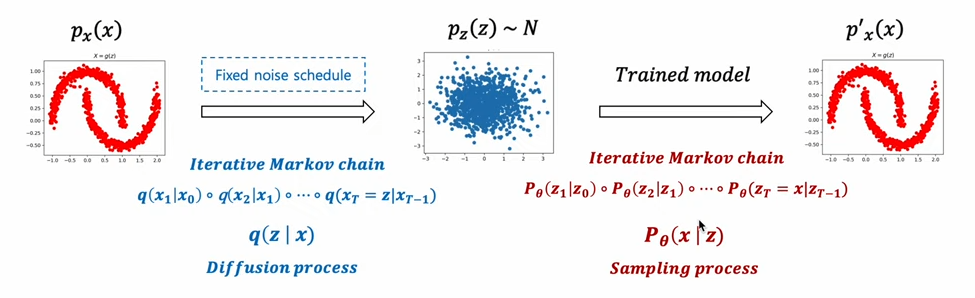
[1] forward 과정을 학습 대상으로 상정하지 않는다. 대신 사전에 정의된 schedule에 따라서 noise를 서서히 주입해가는 과정. -> 학습 대상은 오직 'Sampling process'다.
[2] Diffusion process, Sampling process 모두 조건부 확률 분포의 chain으로 이루어져 있다. (이전 state를 기반으로 다음 state를 상정한다.)
3. Diffusion model
(1) Diffusion model overview
학습된 모델의 패턴을 latent variable로 생성해낸다. 패턴을 학습하기 위해 먼저 패턴을 무너뜨린다.(Noising) 그리고 무너진 패턴을 다시 복원하여 원래의 패턴으로 복원한다.(Denoising, Reverse process)


-> [파란색 분포]를 [빨간색 분포]로부터 다이렉트하게 변환할 수는 없다. 따라서 학습이 필요하다.
-> 다만 [빨간색 분포]가 가우시안 조건부 분포를 따른다면, [파란색 분포]도 가우시안을 따른다.
-> 어떠한 분자가 퍼져나갈 때, 확산될 때, 분자의 다음 위치는 가우시안 분포 안에서 결정된다. 충분히 작은 sequence에서의 확산은 forward와 reserve 모두 물리적으로 가우시안일 수 있다. 분자의 운동이 brown 운동? 이라고 한다.
아래와 같은 근사화가 이루어진다면, noisy한 t 상태를 받아서 덜 noisy한 (t-1) 상태를 조건부 분포로 만들어내는 denoising 과정을 수행할 수 있다.
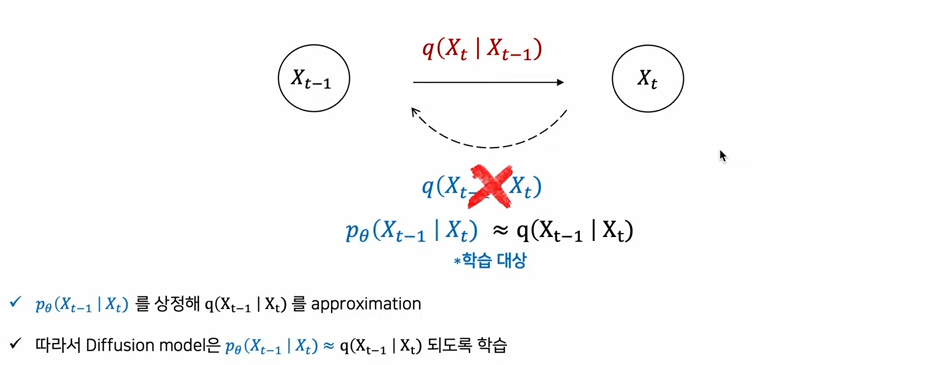
또한 diffusion model은 Noising, Denoising을 여러 스텝으로 잘게 쪼개서 구성한다. 스텝을 잘게 쪼개서 [큰 변화]를 [매우 작은 변화 여러 개]로 만들어 학습을 쉽게 한다. 결국 large numver of small perturbations를 추정하는 것이다.

(2) Diffusion Process (Forward)
가우시안 노이즈가 주입되는 크기는 B(베타)로 사전에 정의된다. t번째에 주입된 노이즈의 크기 Bt다.


-> noise Bt는 분산과 평균에 각각 녹아들게 된다. Bt가 커지면서, 조건부 가우시안 분포의 분산 또한 그에 비례해 커진다.
-> T 시점에 가면, 가우시안 노이즈와 같은 분포를 이루게 된다.

-> 약간의 이전 값 Xt-1을 감소시키면서, 약간의 노이즈 Bt*I를 더하면 Xt가 된다.
-> variance를 계속 1로 맞춰주기 위해 1-Bt, Bt와 같이 파라미터를 사용하였다.
Bt는 점진적으로 커지도록 설계된다. 이는 크게 3가지 방법으로 수행된다.

-> start, end가 Bt의 시작점 및 끝점이다. (0과 1 사이 매우 작은 값들이다.)
-> 참고로, 논문에서는 B1 = 0.0001에서 BT = 0.02로 설정해두었다. (linear하게 올라가는 계수다.)

아래는 Diffusion process 자체의 코드다. 이전 시점인 (t-1)을 조건부로 (t) 시점을 가져가는 가우시안 분포다.

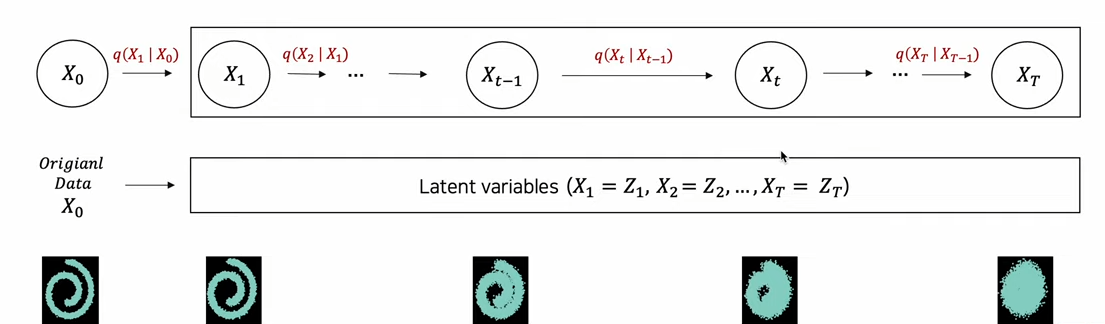
latent variable의 시점에서도 살펴보자. Diffusion process는 latent variable을 많이 가져가는 모델이다. 최초 input인 X0를 제외한 다른 모든 값들을 Latent variables로 간주한다. X1은 X0를 넣은 조건부 가우시안 분포에서 뽑아낸 새로운 latent variable이다. 이처럼 다수의 Latent variables를 가져간다.
Diffusion process는 conditional Gaussian의 joint distribution으로, X0를 기반으로 X1부터 XT까지의 Latent variables을 생성하는 과정이다.
(3) Reverse process
Denoising 과정, 학습의 대상이다.

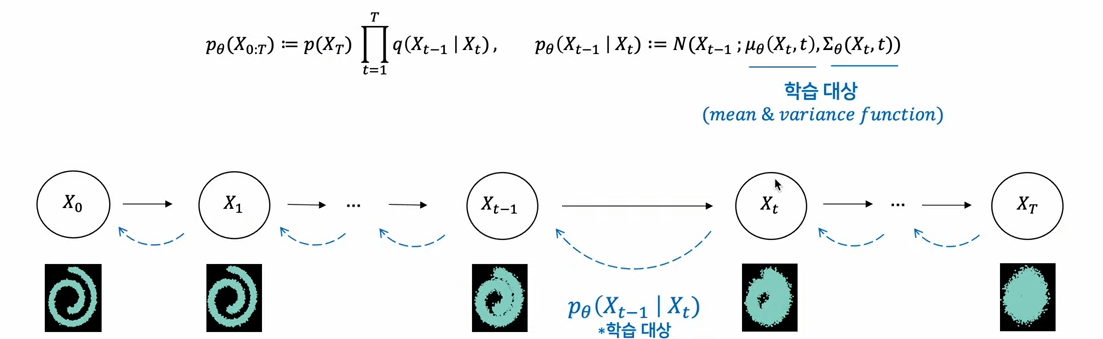

-> forward와 동일하게 reverse에서도 Markov chain을 활용하여, 아래와 같은 식을 얻을 수 있다.
Diffusion process와 마찬가지로, Reverse process도 가우시안 분포가 된다. 전자는 (사전에 정의한 노이즈 크기인) Bt에 의해서 평균과 분산 정의된다. 즉 우리가 알고 있고, 만들 수 있는 분포다. 후자는 우리가 알지 못하는 조건부 가우시안 분포다.
아래는 평균과 분산을 학습하는 코드다. 해당 평균, 분산이 Bt를 기준으로 정의된 평균, 분산과 유사해지도록 목적 함수를 정의한다.

Reverse process는 학습의 대상이기에, 학습의 방향을 보여줄 수 있는 Loss를 살펴보자. 다른 생성모델처럼, data estimation 관점에서 data에 대한 fitting이 최대가 되도록 loglikelyhood를 최대화하는 것이 목적이다.




VAE와의 비교를 통해 Loss를 좀 더 깊게 알아보자.

모델의 latent variable 수가 다르다.



-> 녹색 부분 : latent variable을 control할 수 있는 부분.
-> Denoising process : xT에서 x1까지 이어지는 reverse 과정인 denoising process를 학습하도록 가이드하는 Loss term.
p라는 reverse process는 q라는 diffusion process를 최대한 approximation하도록 학습이 된다. 아무튼, 아래 사진처럼 VAE와 비교했을 때, Loss term이 하나 더 있다는 것을 알 수 있다.

4. Denoising Diffusion Probabilistic Model
DDPM에서는 Loss가 간단한 식으로 정의된다. 이렇게 term을 간결화하여 성능이 더욱 향상되었다.

엡실론과 (학습 대상임을 나타내는) 엡실론 세타 간의 차이로 Loss가 구성된다. DDPM의 Loss는 (각 시점 t에서의 노이즈인) 엡실론을 모델이 예측하도록 하는 Loss다.
어떠한 과정을 거쳐 Loss term이 변했는지 살펴보자.
(1) DDPM Loss에서의 변화
[1] 학습 목적 식에서 Regularization term을 제외하였다. 실험을 통해 굳이 이 term을 학습시키지 않아도 isotropic gaussian을 획득할 수 있다는 것을 알아냈다.


[2] Denoising process의 목적식을 재구성하였다. 앞서 Denoising process에서는 조건부 가우시안 분포의 각 시점별 평균과 분산을 모델이 예측해야 한다고 했다. 그러지 말고, 학습 대상인 평균과 분산 중 분산을 제외해서 가져가자.
이미 알고 있는 B(베타)를 활용하여 분산을 대신하자. 학습 대상이었던 분산을 각 시점에 대한 노이즈의 크기로 상수화한다.


-> 알파는 1에서 베타를 뺀 값이고, [알파 바의 t]는 알파를 1에서부터 t까지 곱한 것이다. torch.cumprod로 구현 가능.
-> [알파 바의 t-1]은 alphas_bar_prev = F.pad(alphas_bar[:-1], (1,0), value=1.).to(device)로 구현 가능.
기존의 Denoising process를 mean function 관점에서 다시 작성하면 아래와 같다. q, p를 학습 대상의 모수로 각각 정의할 수 있다. 둘 간의 KL divergence는 연두 박스와 같이 mean function의 차이로 정의된다.

-> 둘 다 가우시안이므로, 둘 사이의 KL divergence를 가우시안 분포 간의 KLD로 변형할 수 있다.
그리고, 하나 더 나아가 학습대상인 mean function을 새롭게 parameterization하였다. 이 부분이 DDPM에서 가장 중요한 부분인 Denoising matching 부분이다.

-> 여기서 a(알파)는 이미 알고 있고, x0도 diffusion process 상에서 이미 알고 있는 값이다.
xt, 각 latent variable을 상정했을 때 우리가 학습해야 되는 값은 '엡실론' 하나 뿐이다. 또한 위의 식을 (1)에 대입하여 나온 결과는, 수식 (2)이다.
수식 (2)를 다시 살펴보자. mean function이 학습해야 하는 것은 빨간 언더라인이다. 또한 이 중에서 모르는 값은 '엡실론' 뿐이므로, '엡실론'에 (학습 대상이라는 의미를 가진) 세타 아래첨자 기호를 붙여준다. 수식 (3).

-> 입실론 세타(noise prediction network)를 통해 뮤 세타(평균)을 예측할 수 있다.
수식 (2), (3)을 조합하여 얻은 수식 (4)는 목적함수로, 엡실론에 대한 일종의 MSE Loss 와 같은 구성에 noise로 조합이 된 계수 term이 붙어있는 형식이다.

-> noise를 예측하는 모델만으로, 최종적인 loss가 완성된다. 입실론 세타 항 전체가 xt이다.
DDPM은, 수식 (4)에서 더 단순화시켜 계수 term이 제거된 Loss term 수식 (5)를 얻었다.

-> (5)를 이용한 trainig과정에선 sqrt(알파 바), sqrt(1-알파 바)가 필요하다.
-> (4)의 앞의 계수 항들을 1로 setting하는 게 학습이 잘 된다. (by DDPM, 다른 논문에선 이 값들을 다르게 설정하기도 함)
결론 : DDPM은 fix된 noise scheduling을 최대한 활용하면서, 학습 대상을 간소화하고, xt의 reparametrization을 통해 Loss를 간소화했다. 간소화된 loss가 noise estimation의 형태로 나타났다.
5. Experiments
이미지 생성에 대한 결과다. DDPM의 FID score는 3.17로, unconditional 생성모형 중 가장 높은 sample quality를 보인다. 계수 Term을 제외한 경우(Lsimple)는 제외하지 않은 경우(L)에 비해 NLL이 높지만, Sample quality는 월등히 높음을 확인할 수 있다.

DDPM의 Loss term으로 오기까지 많은 Loss term들이 정의되었다. 수식 (1), (2)는 각각 mean function을 예측하는 가운데, 수식 (2)는 계수가 제거된 상태다. 수식 (3), (4)는 엡실론을 예측하는 가운데, 수식 (4)는 계수가 제거된 상태다.

결론적으로, mean function 예측보다는 엡실론 예측에서 더 성능이 좋았다. 또한 noise scheduling을 학습하는 것보다는 fix된 상태에서 성능이 더 좋았다.
계수 term 제거의 효과는 아래 슬라이드와 같다.

6. DDPM 코드 분석

-> Training : 평균을 예측하기 위해, 결국 노이즈를 예측하는 모델을 만들면 된다는 결론에 도달. 그걸 통해 loss를 학습시키고, noise를 예측하는 네트워크를 학습한다. 즉 이게 noise를 더하는 과정.
-> Sampling : 평균, 분산을 기반으로 수식을 전개하여 학습을 수행한다.

-> 아키텍처 : x0에 정해진 schedule대로 노이즈를 한 번에 입혀서 xt를 만든다. 이걸 Unet에 넣어서, Unet의 timestep t와 xt가 같이 들어가 어떤 노이즈가 더해졌는지 predict하게 된다. time step t는 input으로 들어온 image에 얼만큼의 noise가 끼여 있는지를 알려줄 수 있는 수단이다. t는 positional encoding으로 임베딩을 한다.
DDPM의 알고리즘은 위와 같다. DDPM은 수학적으로 매우 복잡하다. score based generative model이며, forward process와 reverse process가 존재한다. Sampling은 Annealed Langevin dynamic이다.
import : 익숙한 torch 종류의 라이브러리들을 import한다. 실험용으로 적절한 CIFAR10을 사용한다.
import torch
import torch.nn as nn
from torch.nn import init
import torch.nn.functional as F
import math
from torchvision.datasets import CIFAR10
from torchvision import transforms
from google.colab.patches import cv2_imshow
if torch.cuda.is_available():
device = torch.device('cuda:0')
else:
torch.device("cpu")
print(" > Device: ", device)
Coeeficient for DDPM : DDPM에서 학습에 필요한 계수들을 설정해준다. 이 모든 값들을 T에 대해서 1에서부터 1000까지 갖고 있다면, 학습이나 샘플링 때 필요한 t에 맞게 index를 모아 와서 해당 계수들과 곱해주면 된다.

T = 1000
betas = torch.linspace(1e-4, 0.02, T).to(device)
alphas = (1. - betas).to(device)
alphas_bar = torch.cumprod(alphas, dim=0).to(device)
alphas_bar_prev = F.pad(alphas_bar[:-1], (1, 0), value=1.).to(device)
# for training
sqrt_alphas_bar = torch.sqrt(alphas_bar).to(device)
sqrt_one_minus_alphas_bar = torch.sqrt(1. - alphas_bar).to(device)
# for sampling
reciprocal_alphas_sqrt = torch.sqrt(1. / alphas_bar).to(device)
reciprocal_alphasm1_sqrt = torch.sqrt(1. / alphas_bar - 1.).to(device)
posterior_mean_coef1 = torch.sqrt(alphas_bar_prev) * betas / (1. - alphas_bar).to(device)
posterior_mean_coef2 = torch.sqrt(alphas) * (1. - alphas_bar_prev) / (1. - alphas_bar).to(device)
sigmas = (betas * (1. - alphas_bar_prev) / (1. - alphas_bar)).to(device)
# for sampling2
reciprocal_alphas_sqrt_ = torch.sqrt(1. / alphas).to(device)
eps_coeff = (betas / torch.sqrt(1. - alphas_bar)).to(device)
Training : [1] x0는 q(x0)에서 샘플링한다고 하는데 그냥 train 함수의 입력 파라미터에 x_0를 가져오라는 의미다.[2] t는 T에서 1까지 uniform하게 뽑으라는데 배치마다 0에서 999 사이의 아무 정수형 숫자를 뽑는다. 예를 들어, 배치 사이즈가 4면 t = [134, 545, 34, 886] 등의 랜덤 숫자 4개가 뽑힐 것이다. [3] 입실론을 가우시안 분포에서 뽑으라는데 입실론은 데이터 이미지와 같은 dimension으로 필요하기 때문에 randn_like함수를 사용하여 같은 shape를 유지한다. [4] 세타가 붙은 함수가 딥러닝 모델이다. x_t라는 변수에 계산된 값이다. 배치마다 t 숫자가 다르므로 gather and expand 함수를 사용한다. 특정 인덱스에서의 계수 값을 가져오기 위해 torch.gather 함수를 사용하고, x_0의 shape에 맞게 곱해질 수 있도록 view 함수를 통해 reshape 작업을 진행한다. 아무튼 이러한 진행을 통해 딥러닝 모델의 입력인 'x_t'를 얻는다. [5] x_t를 딥러닝 모델에 통과시킨 결과와, epx(입실론) 간의 MSE를 loss로 두고, loss를 리턴한다.
Sampling : [1] t는 T에서 1까지 숫자가 줄어들면서 반복하므로, reverse for문을 돌린다. 참고로 torch.full 함수는 첫번째 인자의 shape로 두 번째 인자의 값을 채운 tensor를 만든다. [2] z는 t가 1 이상이면 가우시안 노이즈고, t가 0이면 0이다. [3] 샘플링 땐 t의 계수가 필요하므로 gathe_and_expand()를 사용한다. 사실, 특정 t의 계수가 필요한 것이라 굳이 안 써도 된다. [4] x_t는 방금 계산한 두 항을 더해서, 자기 자신에게 반복 대입하게 한다. [5] 반복문이 끝나면 최종 x_t를 결과로 리턴한다.


def gather_and_expand(coeff, t, xshape):
B, *dims = xshape # Batch size, and remainder
coeff_t = torch.gather(coeff, index=t, dim=0)
return coeff_t.view([B] + [1]*len(dims))
def train(model, x_0):
t = torch.randint(T, size=(x_0.shape[0], ), device=x_0.device)
eps = torch.randn_like(x_0)
x_t = gather_and_expand(sqrt_alphas_bar, t, x_0.shape) * x_0 + \
gather_and_expand(sqrt_one_minus_alphas_bar, t, x_0.shape) * eps
loss = F.mse_loss(model(x_t, t), eps)
return loss
def sample(model, x_T):
x_t = x_T
for time_step in reversed(range(T)):
t = torch.full((x_T.shape[0], ), time_step, dtype=torch.long, device=device)
eps = model(x_t, t)
x0_predicted = gather_and_expand(reciprocal_alphas_sqrt, t, eps.shape) * x_t - \
gather_and_expand(reciprocal_alphasm1_sqrt, t, eps.shape) * eps
mean = gather_and_expand(posterior_mean_coef1, t, eps.shape) * x0_predicted + \
gather_and_expand(posterior_mean_coef2, t, eps.shape) * x_t
z = torch.randn_like(x_t) if time_step else 0
var = torch.sqrt(gather_and_expand(sigmas, t, eps.shape)) * z
x_t = mean + var
x_0 = x_t
return x_0
Model architecture : downsample하면서 분석하고, upsample하면서 원래 사이즈로 만드는 모델이다.
class Swish(nn.Module):
def forward(self, x):
return x * torch.sigmoid(x)
class TimeEmbedding(nn.Module):
def __init__(self, T, d_model, dim):
assert d_model % 2 == 0
super().__init__()
emb = torch.arange(0, d_model, step=2) / d_model * math.log(10000)
emb = torch.exp(-emb)
pos = torch.arange(T).float()
emb = pos[:, None] * emb[None, :]
emb = torch.stack([torch.sin(emb), torch.cos(emb)], dim=-1)
emb = emb.view(T, d_model)
self.timembedding = nn.Sequential(
nn.Embedding.from_pretrained(emb),
nn.Linear(d_model, dim),
Swish(),
nn.Linear(dim, dim),
)
self.initialize()
def initialize(self):
for module in self.modules():
if isinstance(module, nn.Linear):
init.xavier_uniform_(module.weight)
init.zeros_(module.bias)
def forward(self, t):
emb = self.timembedding(t)
return emb
class DownSample(nn.Module):
def __init__(self, in_ch):
super().__init__()
self.main = nn.Conv2d(in_ch, in_ch, 3, stride=2, padding=1)
self.initialize()
def initialize(self):
init.xavier_uniform_(self.main.weight)
init.zeros_(self.main.bias)
def forward(self, x, temb):
x = self.main(x)
return x
class UpSample(nn.Module):
def __init__(self, in_ch):
super().__init__()
self.main = nn.Conv2d(in_ch, in_ch, 3, stride=1, padding=1)
self.initialize()
def initialize(self):
init.xavier_uniform_(self.main.weight)
init.zeros_(self.main.bias)
def forward(self, x, temb):
_, _, H, W = x.shape
x = F.interpolate(
x, scale_factor=2, mode='nearest')
x = self.main(x)
return x
class AttnBlock(nn.Module):
def __init__(self, in_ch):
super().__init__()
self.group_norm = nn.GroupNorm(32, in_ch)
self.proj_q = nn.Conv2d(in_ch, in_ch, 1, stride=1, padding=0)
self.proj_k = nn.Conv2d(in_ch, in_ch, 1, stride=1, padding=0)
self.proj_v = nn.Conv2d(in_ch, in_ch, 1, stride=1, padding=0)
self.proj = nn.Conv2d(in_ch, in_ch, 1, stride=1, padding=0)
self.initialize()
def initialize(self):
for module in [self.proj_q, self.proj_k, self.proj_v, self.proj]:
init.xavier_uniform_(module.weight)
init.zeros_(module.bias)
init.xavier_uniform_(self.proj.weight, gain=1e-5)
def forward(self, x):
B, C, H, W = x.shape
h = self.group_norm(x)
q = self.proj_q(h)
k = self.proj_k(h)
v = self.proj_v(h)
q = q.permute(0, 2, 3, 1).view(B, H * W, C)
k = k.view(B, C, H * W)
w = torch.bmm(q, k) * (int(C) ** (-0.5))
assert list(w.shape) == [B, H * W, H * W]
w = F.softmax(w, dim=-1)
v = v.permute(0, 2, 3, 1).view(B, H * W, C)
h = torch.bmm(w, v)
assert list(h.shape) == [B, H * W, C]
h = h.view(B, H, W, C).permute(0, 3, 1, 2)
h = self.proj(h)
return x + h
class ResBlock(nn.Module):
def __init__(self, in_ch, out_ch, tdim, dropout, attn=False):
super().__init__()
self.block1 = nn.Sequential(
nn.GroupNorm(32, in_ch),
Swish(),
nn.Conv2d(in_ch, out_ch, 3, stride=1, padding=1),
)
self.temb_proj = nn.Sequential(
Swish(),
nn.Linear(tdim, out_ch),
)
self.block2 = nn.Sequential(
nn.GroupNorm(32, out_ch),
Swish(),
nn.Dropout(dropout),
nn.Conv2d(out_ch, out_ch, 3, stride=1, padding=1),
)
if in_ch != out_ch:
self.shortcut = nn.Conv2d(in_ch, out_ch, 1, stride=1, padding=0)
else:
self.shortcut = nn.Identity()
if attn:
self.attn = AttnBlock(out_ch)
else:
self.attn = nn.Identity()
self.initialize()
def initialize(self):
for module in self.modules():
if isinstance(module, (nn.Conv2d, nn.Linear)):
init.xavier_uniform_(module.weight)
init.zeros_(module.bias)
init.xavier_uniform_(self.block2[-1].weight, gain=1e-5)
def forward(self, x, temb):
h = self.block1(x)
h += self.temb_proj(temb)[:, :, None, None]
h = self.block2(h)
h = h + self.shortcut(x)
h = self.attn(h)
return h
class UNet(nn.Module):
def __init__(self, T, ch, ch_mult, attn, num_res_blocks, dropout):
super().__init__()
assert all([i < len(ch_mult) for i in attn]), 'attn index out of bound'
tdim = ch * 4
self.time_embedding = TimeEmbedding(T, ch, tdim)
self.head = nn.Conv2d(3, ch, kernel_size=3, stride=1, padding=1)
self.downblocks = nn.ModuleList()
chs = [ch] # record output channel when dowmsample for upsample
now_ch = ch
for i, mult in enumerate(ch_mult):
out_ch = ch * mult
for _ in range(num_res_blocks):
self.downblocks.append(ResBlock(
in_ch=now_ch, out_ch=out_ch, tdim=tdim,
dropout=dropout, attn=(i in attn)))
now_ch = out_ch
chs.append(now_ch)
if i != len(ch_mult) - 1:
self.downblocks.append(DownSample(now_ch))
chs.append(now_ch)
self.middleblocks = nn.ModuleList([
ResBlock(now_ch, now_ch, tdim, dropout, attn=True),
ResBlock(now_ch, now_ch, tdim, dropout, attn=False),
])
self.upblocks = nn.ModuleList()
for i, mult in reversed(list(enumerate(ch_mult))):
out_ch = ch * mult
for _ in range(num_res_blocks + 1):
self.upblocks.append(ResBlock(
in_ch=chs.pop() + now_ch, out_ch=out_ch, tdim=tdim,
dropout=dropout, attn=(i in attn)))
now_ch = out_ch
if i != 0:
self.upblocks.append(UpSample(now_ch))
assert len(chs) == 0
self.tail = nn.Sequential(
nn.GroupNorm(32, now_ch),
Swish(),
nn.Conv2d(now_ch, 3, 3, stride=1, padding=1)
)
self.initialize()
def initialize(self):
init.xavier_uniform_(self.head.weight)
init.zeros_(self.head.bias)
init.xavier_uniform_(self.tail[-1].weight, gain=1e-5)
init.zeros_(self.tail[-1].bias)
def forward(self, x, t):
# Timestep embedding
temb = self.time_embedding(t)
# Downsampling
h = self.head(x)
hs = [h]
for layer in self.downblocks:
h = layer(h, temb)
hs.append(h)
# Middle
for layer in self.middleblocks:
h = layer(h, temb)
# Upsampling
for layer in self.upblocks:
if isinstance(layer, ResBlock):
h = torch.cat([h, hs.pop()], dim=1)
h = layer(h, temb)
h = self.tail(h)
assert len(hs) == 0
return h
model = UNet(T=T, ch=128, ch_mult=[1, 2, 2, 1], attn=[1],
num_res_blocks=2, dropout=0.1).to(device)
#ema_model = copy.deepcopy(model)
optim = torch.optim.Adam(model.parameters(), lr=2e-4)
#sched = torch.optim.lr_scheduler.LambdaLR(optim, lr_lambda=warmup_lr)
Train iteration : [1] 학습하고, 전체 데이터셋을 한 번 다 훑어볼 때마다 sample을 뽑게 한다. [2] 일반적인 딥러닝 구조와 동일하게 loss 구해서 optimaze한다. [3] 샘플링 시 random한 noise를 배치 사이즈 5로 준비해서 샘플 함수에 집어 넣어 이미지 결과를 얻는다. 그걸 출력한다.
-> training 결과 : 딥러닝을 통과시킨 결과와 입실론과의 MSE, error를 리턴한다.
-> Sampling 결과 : xt를 반복반복한 후 최종 결과 x0를 리턴한다.
7. DDPM 한 번 더
노이즈를 단계별로 조금 조금씩 더한다. 특정 스텝으로 한 번에 노이즈를 더할 수 있지 않을까? 이게 DDPM의 주된 시도다. 따라서 샘플링을 할 때, xt를 x0에 대해 한 번에 계산할 수 있는 수식을 사용한다. 즉, x0 한 장을 가지고 xt를 샘플링할 수 있다.

우리가 목표로 하는 것은 noise에서 image로 돌아오는 reverse step이다. 단계, 단계가 매우 작기 때문에 reverse step 또한 가우시안일 것이다. 즉, reverse process로 가우시안으로 모델링 가능하다. 따라서 그 안의 평균과 분산을 학습할 것이다.

-> Low freq : 어떤 contents가 생성될 지, High freq : 이미지의 디테일한 정보가 추가되는 단계.
[왜 q가 가우시안으로 표현되는가]

-> 간단하게 베이즈 정리 사용 후, 각각 모두 가우시안 노이즈이므로 가우시안 식으로 다 풀어서 쓴다. 정리하여 평균과 분산을 구하자.
[ More about ]
-> Bt(베타_t)를 기존의 값이 아닌 새로운 값이나, 새로운 공식에 대입하여 넣는 경우도 존재한다.
-> DDPM에선 분산을 Bt와 동일한 값으로 설정하였는데, 이에 대한 변경도 연구 주제 중 하나다.
참고해볼 시뮬 링크 : https://github.com/acids-ircam/diffusion_models
출처 링크 : https://www.youtube.com/watch?v=_JQSMhqXw-4
출처 링크 2 : https://www.youtube.com/watch?v=svSQhYGKk0Q
출처 링크 3 : https://www.youtube.com/watch?v=uFoGaIVHfoE
'LAB > 생성형 AI' 카테고리의 다른 글
| 생성모델(3) Denoising Diffusion Implicit Models(DDIM) (1) | 2024.01.08 |
|---|---|
| 생성모델(2) Neural ODE (1) | 2024.01.08 |
| 생성모델(5) conditional generation (0) | 2023.12.28 |
| 생성모델(4) Score-based generative models (2) | 2023.12.28 |
| Diffusion_Toy Simulation code 분석 (0) | 2023.07.12 |



