1. DDIM
(1) from DDPM
DDPM은 퀄리티가 좋으며, 다양한 이미지를 생성한다. 데이터의 분포 가 주어질 때 모델 분포 가 를 근사하도록 학습한다. 또한 파라미터 θ는 variational lower bound를 최대화시키는 방향으로 학습된다. 는 잠재 변수에 대한 inference distribution이며, DDPM은 을 고정시키고 학습을 진행한다. 또한 감소 수열 로 매개변수화된 Gaussian transition이 있는 다음의 Markov chain을 사용한다. 그러나 DDPM은 sampling 속도가 비교적 느려, 생성 속도가 더딘 편이다. Diffusion model의 생성 속도를 개선하기 위한 방법 중 하나가 DDIM이다.
non-Markovian diffusion process다. 생성 모델은 inference process의 역과정으로 근사되므로 생성 모델에 필요한 iteration의 수를 줄이기 위해 inference process를 다시 생각하자. DDPM의 경우, 목적 함수 가 주변 분포 에만 의존하며 결합 분포 에는 직접적으로 의존하지 않는다. 따라서 non-Markovian인 새로운 inference process가 필요하며, 이에 대응되는 새로운 generative process가 필요하다.
(2) Variational Inference for non-Markovain Forward Processes

Non-Markovian diffusion process를 시도하였다. sampling 단계만 변경되었고, 나머지는 동일하다. 그 전 단계인 x1과 원본인 x0를 사용하여 x2를 표현할 수 있다. 같은 원리로 x2, x0를 given으로 x3이 표현 가능하다.
[1] Non-Markovian forward processes : 실수 벡터 에 대한 inference distribution 은 아래와 같다.

에 대하여
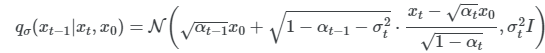
베이즈 정리에 의해 forward process는 다음과 같으며, 이 또한 가우시안 분포다. xt가 xt-1과 x0에 의존하므로 DDIM의 forward proess는 Markovian chain이 아니다.

-> DDPM에선 q 값을 구하기 위해 베이즈정리와 가우시안의 평균, 분산을 다 구해서 정의를 내렸다. DDIM은 바로 이전 스텝과 x0, 이 2개의 given으로 다음 스텝을 정의내리면 가우시안 distribution 정의를 내릴 수 있다.
[2] Generative Process and Unified Variational Inference Objective : 학습 가능한 generative process 를 정의한다. 가 주어지면 먼저 대응되는 을 예측하고 이를 이용하여 로 을 샘플링한다.
우선 xt를 아래와 같이 정의하고, 모델 ϵ(t)^θ(xt)가 x0에 대한 정보 없이 xt로부터 ϵt를 예측한다. 식을 다음과 같이 다시 세우면 주어진 xt에 대한 x0의 예측인 denoised observation을 예측할 수 있다.


고정된 prior 에 대한 generative process는 아래와 같다. generative process가 모든 t에서 성립하도록 t=1인 경우에 약간의 Gaussian noise를 추가한다.

파라미터 θ는 다음 목적 함수로 최적화된다. 의 정의를 보면 에 따라 목적 함수가 다르기 때문에 다른 모델이 필요하다는 것을 알 수 있다.


-> 추가자료에 대한 설명 : J
(3) Sampling from Generalized Generative Processes
pre-trained DDPM을 새로운 목적 함수에 대한 해로 사용할 수 있으며 를 변경하여 필요에 따라 샘플을 더 잘 생성하는 generative process를 찾는 데 집중할 수 있다.
[1] Denoising Diffusion implicit models : xt로부터 xt-1를 생성하는 식이다. 는 에 독립적인 가우시안 noise이며, 로 정의한다. 를 변경하면 같은 모델 를 사용하여도 generative process가 달라지기 때문에 모델을 다시 학습하지 않아도 된다.

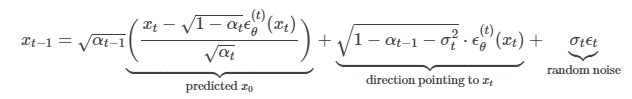
모든 t에 대하여 아래와 같이 정의한다면, generative proces가 DDPM이 된다.

모든 에 대하여 으로 두면, 주어진 와 에 대하여 forward process가 deterministic해진다. 이 경우 부터 까지 모두 고정되어 샘플링되기 때문에 implicit probabilistic model이 된다. 이는 DDPM 목적 함수로 학습된 implicit probabilistic model이기 때문에 Denoising Diffusion Implicit Model (DDIM)이라 부른다.
[2] Accelerated generation processes : DDPM은 forward process가 T setp으로 고정되어 있기 때문에 generative process도 T step으로 강제된다. 반면 DDIM의 목적함수 L1은 가 고정되어 있는 한 특정 forward 방식에 의존하지 않으므로 T보다 작은 길이의 forward process들도 고려할 수 있다. Forward process를 로 정의하지 않고 부분 집합 로 정의하자. 여기서 는 길이가 의 부분 수열이다. 특히 )가 주변 분포에 일치하도록 에 대한 forward process를 정의한다. 그러면 generative process는 를 뒤집어 샘플링하는 것이고, 이를 샘플링 궤적(trajectory)이라 한다. 샘플링 궤적의 길이가 보다 짧을수록 샘플링 과정의 계산 효율이 상당히 증가한다.
[3] Relevance to Neural ODEs : DDIM 샘플링 식을 다음과 같이 다시 쓸 수 있으며, 상미분방정식 ODE를 풀기 위한 Euler intergration과 비슷해진다.


σ를 어떤 값으로 두냐와 상관없이 학습해야 하는 parameter는 θ다. markovian process로 학습시킨 pretrained DDPM model의 parameter θ를 DDIM의 generative process에도 이용할 수 있게 된다. 즉 DDIM은 새로운 훈련 방법을 제시했다기보다는 diffusion process의 목적 함수를 non-markovian chain으로 일반화하고, 좀 더 빠르게 이미지 생성이 가능하도록 새로운 sampling 방법을 제시한 것이다.
요즘 트렌드는 DDPM으로 학습시킨 모델을 DDIM의 generation 방식으로 sampling하는 방식이다. 좋은 성능의 DDPM 모델을 이용하면서도 이미지를 빠르게 sampling할 수 있다.
-> DDPM에선 q 값을 구하기 위해 베이즈정리와 가우시안의 평균, 분산을 다 구해서 정의를 내렸다. DDIM은 바로 이전 스텝과 x0, 이 2개의 given으로 다음 스텝을 정의내리면 가우시안 distribution 정의를 내릴 수 있다.
-> random noise가 시그마t와 묶여져 있는데, 시그마t = 0으로 두면 noise가 없어진다. 즉 좀 더 deterministic generative한 process를 가지게 된다. 또한 확률적인 변수가 없어지게 되므로 noise와 image가 거의 1대 1 매칭이 될 것이다. 빠른 샘플링이 가능하다.
2. How to solve the generative SDE or ODE in practice?
ODE와 SDE, ODE는 1대 1 매칭이 확연한 편이다.


출처 : https://www.youtube.com/watch?v=uFoGaIVHfoE&t=5199s
출처2 : https://kimjy99.github.io/%EB%85%BC%EB%AC%B8%EB%A6%AC%EB%B7%B0/ddim/
'LAB > 생성형 AI' 카테고리의 다른 글
| 생성모델(2) Neural ODE (1) | 2024.01.08 |
|---|---|
| 생성모델(1) Denoising Diffusion Probabilistic Models(DDPM) (2) | 2024.01.08 |
| 생성모델(5) conditional generation (0) | 2023.12.28 |
| 생성모델(4) Score-based generative models (2) | 2023.12.28 |
| Diffusion_Toy Simulation code 분석 (0) | 2023.07.12 |



