1. Overview
[1] 데이터 공간 상에서 임의의 랜덤한 노이즈(데이터)를 생성한다. [2] 확률 밀도 함수의 기울기를 계산 후, 확률 값이 높아지는 방향으로 데이터를 업데이트한다. [3] 확률값이 높은 곳에 도달하면 샘플링된 데이터와 유사한 데이터를 생성한다.

2. Score-based generative models
score란 확률 밀도 함수의 미분이다. 즉, 입력 데이터 x에 대한 미분이다.

입력 데이터와 score의 dimension이 동일하다.
[1] 데이터의 분포를 모르지만 Score만 알면 데이터 생성이 가능하다. [2] Score를 데이터로부터 추정한다. (score matching, training) [3] 추정된 score를 바탕으로 새로운 데이터를 sampling한다. (langevin dynamics, testing)

(1) Score matching
데이터 x에 대해 score 값을 계산해주는 모델(Score Network)를 만들자.


(2) Score network
score network의 학습과정은 다음과 같다. 주어진 data에 약간의 노이즈를 추가해준다. 노이즈가 추가된 data가 network의 input이 되고, output은 해당 데이터의 score이다. U-net을 활용하여 score network를 구성한다.

(3) Langevin dynamics
추정된 score를 바탕으로 sample을 찾아가는 과정. score network가 잘 학습되었다면, 모든 데이터 공간상에서 score를 계산할 수 있다. 임의의 데이터 (랜덤 노이즈)에서 시작하여, 현재 시점에서 추정된 score를 기반으로 데이터를 업데이트한다. score를 타고 올라가다 보면 높은 확률값의 데이터를 생성 가능하다.

3. NCSN(Noise Conditional Score Network)
(1) Noise conditional score networks
확률값이 낮은 공간에서 score 추정이 부정확하다는 문제점 때문에, 데이터에 노이즈를 추가한 후 score를 추정하도록 한다. 노이즈가 추가된 데이터가 확률값이 낮은 공간을 채워 score 추정이 가능하다.

(2) NCSN
input에 데이터와 노이즈의 크기가 들어가고, 뭐 그렇다.


3. DDPM
(1) MLE
생성 모델은 모집단의 분포를 추정하는 것이 목적이며, 분포 추정의 기본이 되는 방식은 MLE(Maximum Likelihood Estimation)이다. [1] 샘플링된 데이터를 모집단으로부터 전달받는다. [2] 데이터들이 해당 분포로부터 샘플링되었을 확률(pdf)을 계산한다. [3] pdf값을 모두 곱해주면 likelihood 값이 나온다. 주어진 파라미터들이 실제 데이터 분포일 때, ~~. [4] Likelihood가 더 큰 값이 원데이터와 유사한 분포다.

그러나 이처럼 모든 likelihood 값을 구할 수 없으므로, likelihood를 파라미터로 미분한 후 0 값이 되는 지점에만 집중한다. 즉 뮤(평균), 시그마(분산)의 MLE를 통해 값들을 계산한다.

(2) DDPM
VAE와 loss 식이 유사하다.


우리의 목표는 gaussian distribution을 추정하는 모델을 만드는 것이다. [1] xT와 사전에 정의한 분포가 동일하도록 하는 loss term, [2] reverse process를 학습한 loss term, [3] x0로 나가는 loss term이다.
DDPM의 최종 목적은 gaussain distribution의 평균 뮤 값을 추정하는 모델을 만드는 것이다.
reverse process 하나의 평균을 optimization하는 것이 목표로 식이 전개된다.

(3) algorithm
[1] training 과정이다. 노이즈를 얼만큼 입힐 지 미리 정의를 내리는 단계.

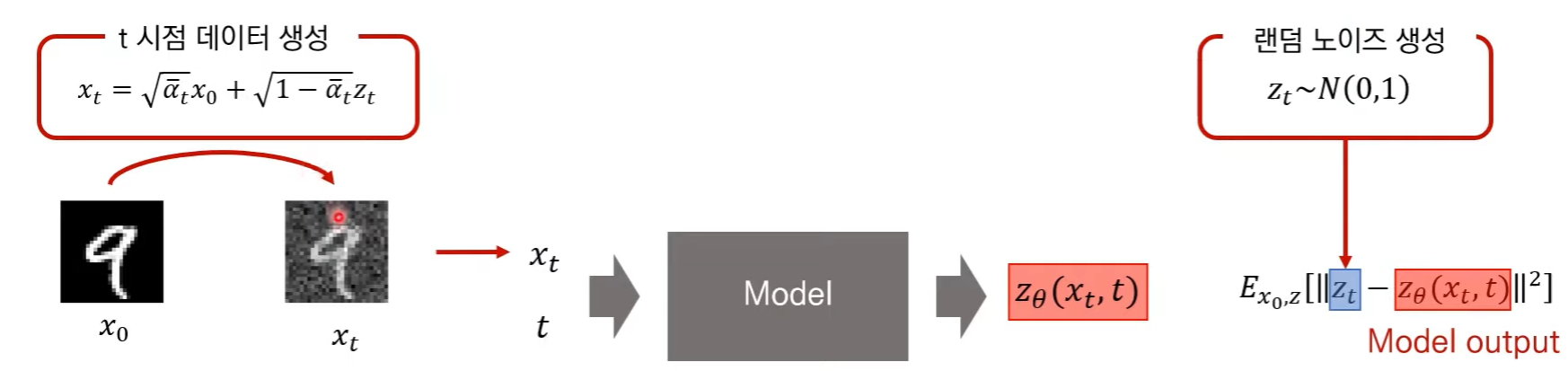
[2] Sampling과정이다. 각각 time step에서 어떤 평균과 분산을 지니는지 학습하는 단계.


4. NCSN과 DDPM의 유사점
(1) Training : 목적식이 유사하다.

(2) generating : 데이터를 생성하는 식이 유사하다.

(3) ODE and SDE
방정식을 푼다 = 식이 주어지고, 그 식의 해를 구하는 과정을 의미한다. 또한 미분 값이 포함되어 있는 형태의 방정식을 미분 방정식이라 한다. 미분 방정식 ODE(Ordinary Differential Equation)은 적분을 취하여 푸는 것이 가장 단순한 방법이다. ODE를 푼다는 것은 어떤 함수를 구한다는 의미다.

미분 방정식의 일종이라 할 수 있는 SDE(Stochastic Differential Equation)은 ODE에서 randomness가 추가된 버전이다. SDE를 푼다는 것은 어떤 Random process Xt를 찾는 것을 의미한다.

(4) Score-based Generative Modeling with SDEs

continuous하게 노이즈를 추가 및 제거한다. 노이즈 제거하는 reverse SDE 과정에서 score function이 사용된다. [1] forward과정에서 dx를 구하면 다음과 같다. 여기서 첫번째 항은 ODE과 같이 방향을 결정하는 drift term이고, 두번째 항은 diffusion term으로 랜덤성을 부여하는 항이다. 또한 마지막에 f(t)과 g(t)를 이용하여 SDE의 special case로 일반화하였다. NSCN 역시 SDE의 다른 special case로 정의될 것이다.



[2] reverse 과정은 아래와 같이 forward 과정과 1대 1 매칭이 된다. 이는 1982년 논문을 통해 도출된 식이다. score function이 사용됨을 알 수 있다.

[3] score function은 어떻게 얻을까? neural network를 가지고 score function을 바로 학습하는 방법이 있다. 중간 time step의 xt를 알 수 없기 때문에 dffusion에서 했던 방법처럼 특정 time step의 xt를 x0을 가지고 구할 수 있기 때문에 xt given x0을 가지고 score matching을 수행한다.

x0를 가지고 xt를 re-parametrized sampling할 수 있다. 또한 이를 통해 score function, Neural network model를 학습한다. 여기서 입실론은 '어느 정도 노이즈가 더해졌는가'를 학습하는 것이다.
score based model과 ddpm 모델들은 동일한 loss function logic들을 가지며, 정의된 식들만 살짝 다르다.


결론 : SDE라는 구조 내에서 NCSN과 DDPM을 통합할 수 있다.
순서 : Diffusion 식을 풀어서 쓰다 보니 미분 방정식처럼 쓸 수 있었다. -> 그 미분 방정식을 풀기 위해 reverse SDE 식을 만들어 보니, score function이 필요했다. -> score function을 모델링하여 optimize해보니 (diffusion과 똑같이) 각각의 timestep에 대해 얼만큼 노이즈가 더해졌는지 판별하는 형태였다.
결론 : SDE가 Diffusion 모델과 score based model을 포함하고 있는 더 큰 틀이다.
출처 : https://www.youtube.com/watch?v=d_x92vpIWFM
출처2 : https://www.youtube.com/watch?v=uFoGaIVHfoE&t=5199s
'LAB > 생성형 AI' 카테고리의 다른 글
| 생성모델(1) Denoising Diffusion Probabilistic Models(DDPM) (2) | 2024.01.08 |
|---|---|
| 생성모델(5) conditional generation (0) | 2023.12.28 |
| Diffusion_Toy Simulation code 분석 (0) | 2023.07.12 |
| Generative Model(생성모델) (0) | 2023.06.22 |
| VAE (0) | 2023.06.22 |



