아래의 세미나 내용과 같은 흐름, 같은 순서로 전개됩니다.
1. Abstract [VAE]
두 가지 contribution이 제시된다.
1) Variational lower bound의 reparametrization [standard stochastic gradient method]
2) lower bound estimator를 통해서 (data point당 연속적인 잠재변수를 갖는) i.i.d datasets에서의
posterior를 효과적으로 fitting할 수 있다.
VAE는 생성 모델로써 존재한다.
i.i.d datasets의 datapoint당 연속적인 잠재 변수를 갖는다.
따라서 잠재변수로 datapoint를 생성할 수 있고, datapoint로부터 잠재변수를 이끌어낼 수 있다.
2. Introduction [VAE]
Posterior를 이해하는 과정에서 Evidence를 구할 때 어려움을 겪는다.
이 Evidence에 Variational Inference를 적용하여 ELBO라는 Variational Lower Bound를 알 수 있다.
이 bound에 대하여 Stochastic Gradient를 통해 optimize했다고 생각하면 된다.
3. Deep Neural Networks
Neural network : 사람 뇌에 있는, 신경 세포의 신경 전달 과정을 모방하여 구성한 네트워크
-> 사람 뇌의 뉴런들은 특정 임계값(Threshold) 이상의 자극을 받으면 결과를 전달한다.
-> Neural network는 Input를 받으면, 가중치(Weight)에 따라 Output을 출력한다.
Deep Neural Networks : Hidden layer를 두 개 이상 가지는 Neural network
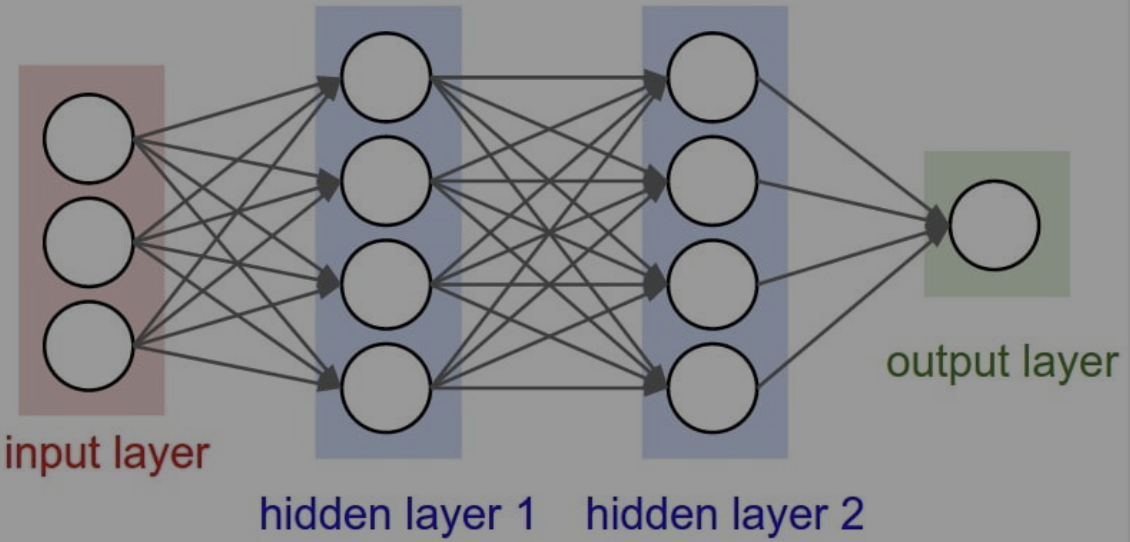
모델 학습을 통해, 모델을 결정짓는 parameter를 결정한다.
모델의 출력 값과 target(정답)과의 차이를 통해 최적의 파라미터를 찾는다.
loss : 예측값과 실제값의 차이, loss가 적을수록 좋다.
-> 차이가 제일 적은 loss를 찾는 방법은 Gradient descent[경사하강법]이다.

Deep Neural Networks에는 2가지 학습 방법이 존재한다.
1) Backpropagation 알고리즘 : MSE 관점, CE 관점
2) MLE(Maximum Likelihood Estimation) 알고리즘 : 확률적 관점에서 해석한 것임
4. Manifold Learning (AE에 사용되는 주요 개념)
Manifold : 고차원 데이터를 저차원에서도 잘 표현하는 공간
Manifold Learning : 차원 축소를 위해 사용된다.
2가지 가정이 있다.
1) 고차원의 데이터 밀도는 낮지만, 이들 집합을 포함하는 저차원의 매니폴드가 존재한다.
2) 이 저차원의 매니폴드를 벗어나는 순간 밀도는 급격히 낮아진다.
(ex) 3차원에서 데이터 100개는 밀도가 낮아 비교적 무의미하지만,
이 100개를 모두 포함한 공간(집합)을 가진 2차원(저차원)의 공간이 존재한다.
이러한 저차원의 공간 내에서는 그 데이터들이 비교적 유의미하게 사용될 수 있다.
그렇다면 차원 축소를 하는 이유는 무엇일까?
1) 차원의 저주
2) 차원의 저주로 인해 [가깝다고 생각되는 고차원 공간에서의 두 샘플들 간의 거리가 실제론 먼 경우] 발생
-> 차원의 저주가 무엇인지 모른다면 여기를 클릭 !!

5. AutoEncoder

입력과 출력이 같은 구조.
비지도 학습 문제를 지도 학습 문제로 바꾸어서 해결.
(비지도 학습 : 정답 라벨이 없는 데이터를 비슷한 특징끼리 군집화하여 새로운 데이터에 대한 결과 예측)
(지도 학습 : 정답이 있는 데이터를 활용해 데이터를 학습시킴)
입력을 기반으로 특징을 추출, 추출된 특징으로 다시 원본 데이터를 출력하는 네트워크
-> 크게 encoder와 decoder, 2가지 파트로 구성된다.
1) input data를 Encoder Network에 통과시켜, 압축된 z값을 얻는다.
2) 압축된 z vector로부터 Input data와 같은 크기의 output data를 생성한다.
3) 이때의 loss값 = [입력값 X]와 [Decoder를 통과한 Y값]의 차이
오토인코더는 Input data의 feature(특징)을 추출할 때 많이 사용된다.
주로 Dimenson Reduction[차원 축소]에 많이 사용된다.
AE를 학습한다면 encoder 관점에선, 최소한의 input data를 잘 복원한다. 최소한의 성능 보장
6. Variational AutoEncoder
Generative model이다.
-> 새로운 data instance들을 생성(Training Data의 distribution을 근사함)한다.
VAE의 최종 목적은?
-> 고양이 데이터가 있다면, [기존 Trainig DB에 가지고 있던 고양이와 유사한 샘플]을 생성하는 것
VAE 네트워크의 학습을 통한 출력 결과
-> Training DB에 있는 데이터 X가 나올 확률을 구하는 것
단순히 샘플을 생성하는 것이 아니다. controll로 생성된 이미지들 ?
-> Generator는 Latent variable z로부터 샘플을 생성한다.
-> controller처럼 이미지를 조정하는 z vector를 추출할 수 있다면?
(ex) 고양이에 [귀여움]의 정도를 조절하여, 귀여운 고양이를 생성하는 원리
-> 결론 : z vector(latent vector)는 controller(제어기)의 역할을 한다.
-> 추가로, 기존 Training DB에 있던 샘플과 유사한 샘플을 생성하기 위해 prior 값을 사용
(prior = P(z), z가 나올 확률을 의미)
7. AE와 VAE의 차이점

-> AE의 목적 : Manifold Learning, Encoder를 학습시키기 위해 Decoder를 이용,~
-> VAE의 목적 : Generative Model, Decoder를 학습시키기 위해 Encoder를 붙임
<또 다른 큰 차이점>
-> AE : prior에 대한 조건이 없다. 의미 있는 z vector의 space가 계속 바뀐다. z 값이 바뀐다.
-> VAE : prior에 대한 condition을 부여. z vector가 prior와 같은 분포를 따른다.
<다시 정리하는 차이점>
-> AE : 잠재 코드(Latent code) 값이 어떤 하나의 값이다.
-> VAE : 잠재 코드(Latent code) 값이 평균, 분산으로 표현되는 어떤 가우시안 분포다.
8. Variational Inference
posterior extimation하는 statistical inference 문제를 optimazation 문제로 바꿔다.
-> prior에서 바로 sampling하지 않는다. (잘못된 결과값이 나옴)
-> 이상적인 sampling 함수를 통해 sampling을 수행한다.
-> 이상적인 sampling 함수를 모르므로 Variational Inference(변분 추론)을 사용한다.
-> Optimization은 posterior estimation 방식보다 훨씬 빠르고, 많은 도구가 있기에 이는 중요한 치환!
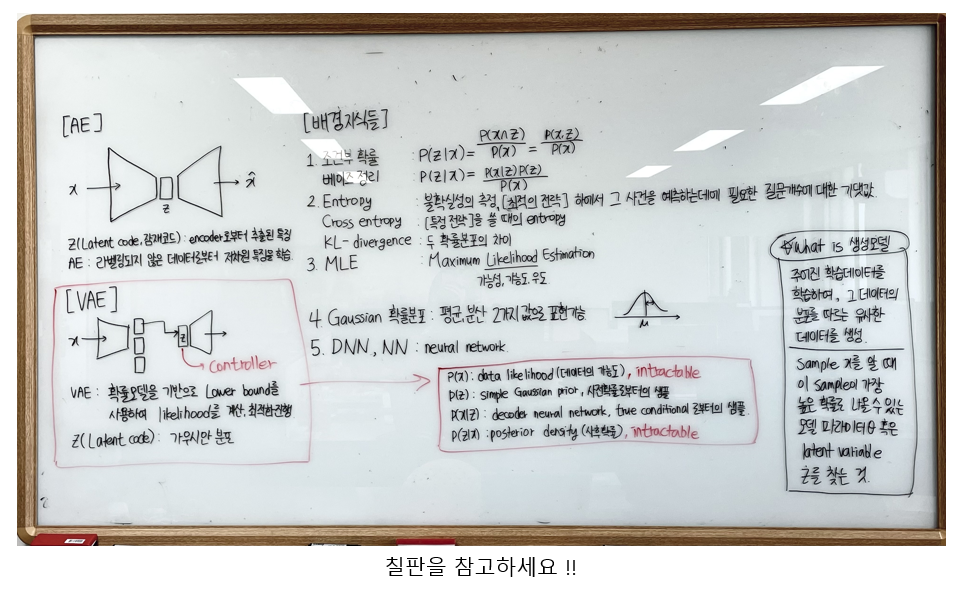
다시 정리해보자면
-> p(x) : data likelihood(데이터의 가능도), intractable
-> p(z) : simple Gaussian prior, 사전 확률로부터의 샘플
-> p(x|z) : decoder neural network, true conditional로부터의 샘플
-> p(z|x) : posterior density(사후 확률), intractable
p(z|x)가 아닌, 이상적인 sampling함수 = qΦ(z|x) 를 추정하고
이상적인 sampling함수가 정의되었다면
z vector로부터 Input x와 유사한 데이터를 생성할 수 있다.
1. log(p(x)) 계산하기

공식은 위의 그림과 같다. p(x)의 최댓값을 구하기 위해 log 값을 씌워준다.
이를 한 줄 씩 유도해보자.


KL값을 최소화해야 한다. 그러나 우리는 (KL공식 안에 들어있는) p(z|x)를 알지 못한다.
KL 값을 최소화하는 대신, ELBO 값을 최대화하자.
-> 이것이 log를 사용하여 log(p(x))를 둘로 쪼갠 이유이다.

2. ELBO 수식 계산하기


한 줄 씩 유도해보자.

3. 결론

-> reconstruction term : 이상적인 샘플링 함수로부터 얼마나 잘 복원했는가
-> regularization term : 이상적인 샘플링 함수가 최대한 prior와 같아지도록 만들어줌
(여러 sample 중, prior와 유사한 값을 샘플링하도록 condition 부여)
-> 두 확률분포 사이의 거리 : 이상적인 샘플링 함수 qΦ(z|x)와 샘플링 함수 p(z|x) 사이 거리
9. Final Optimization Problem

결과적으로 우리가 최적화시킬 값은 'Reconstructin term'과 'regularization term'이다.
이 두 term을 최적화시켜주면, 우리가 원하는 샘플을 얻을 수 있다.
10. ELBO 정리하기 및 요약

-> 우리의 목적 : Generator를 학습시키는 것
-> prior, p(z)만 가지고 학습을 시키면 학습이 잘 되지 않는다.
-> 이상적인 sampling 함수, qΦ(z|x)를 도입하자.
(x를 evidence로 주고, x에 대해서 Generator가 잘 학습할 수 있게 해주는 z를 sampling하기 위해 도입함)
-> [sampling한 값]은 [input 값]과 비슷하길 원한다. (Reconstruction Term)
-> 이는 𝜃를 최적화시키는 MLE 문제로 풀 수 있다.

11. Loss Function

-> reconstruction error : 현재 샘플링용 함수에 대한 negative log likelihood
(xi에 대한 복원 오차, AE 관점)
-> regularization : 현재 샘플링용 함수에 대한 추가 조건
(샘플링의 용의성/ 생성 데이터에 대한 통제성을 위한 조건을 prior에 부여)
(이와 유사해야 한다는 조건을 부여)
12. Reparameterization trick
샘플링 과정에서 Backprop을 진행할 때 문제가 발생한다.
-> NN으로 모델을 정의했으므로 gradient descent(경사하강법) or ascent를 사용할 예정
-> 그러나 sampling은 미분이 가능한 연산이 아니므로, back propagation으로 풀 수 없다.
-> parameter에 대해 미분이 가능한, 즉 모델이 deterministic할 때에만 경사하강법 사용 가능
-> fixed parameter들에 대해 stochasticity는 input에만 있고, 같은 input은 같은 output이 항상 나와야 한다.
그러나 이 'sampling'은 모델 자체에 stochasticity(확률적)가 들어가므로 문제가 된다.
이를 교묘하게 우회하는 방법이 reparameterization trick이다.
이 트릭을 이용하면, 문제없이 Backpropagation이 가능하다.

-> Original : Random node가 모델 안에 들어가 있다.
-> Trick : Random node가 input단에 위치. 모델 안에는 Random이 없다.
Trick 뒷부분은 여길 보고 정리하자.
좀 더 알고싶다면 여기를 클릭 !
13. 최종 정리

-> VAE는 Intractable density를 구사한다.
-> VAE는 여러 수식 전개를 통해서 Lower bound 값을 구할 수 있다.
-> VAE는 확률 모델을 기반으로 했기 때문에, 조금 더 유연하게 계산할 수 있다.
-> Feature map(네트워크 특징맵)을 가지고 다른 일을 수행할 수 있다.
-> but VAE는 density를 직접적으로 구한 것이 아니다. 직접적으로 구하는 모델들보다는 성능이 떨어진다.
'LAB > 생성형 AI' 카테고리의 다른 글
| 생성모델(5) conditional generation (0) | 2023.12.28 |
|---|---|
| 생성모델(4) Score-based generative models (2) | 2023.12.28 |
| Diffusion_Toy Simulation code 분석 (0) | 2023.07.12 |
| Generative Model(생성모델) (0) | 2023.06.22 |
| diffusion model 정리 자료 (0) | 2023.02.22 |



