input space가 연속적/이산적인 것에 대해서는 많이 다뤘다. model space가 연속적/이산적인지를 알아보자.
1. ODE
(1) ODE
딥러닝이란 알려지지 않은 unknown function f를 찾아가는 과정이다. 그 과정에서 y- f(x) = error(loss)를 구해 function을 업데이트한다. 최적화 f(x)를 구하는 매우 직접적인 방식이다.

neural ODE 역시 함수 f(x)를 찾아가겠다는 목적은 동일하다. 그러나 다른 접근으로 찾아간다. DE(Differential Equation)은 미분한 도함수를 포함하는 방정식이다. ODE(Ordinary DE, 상미분 방정식)는 미분하는 변수가 하나인 경우를 말한다.
(2) 미분방정식 ODE를 인공신경망에 가져온 이유는?
sequential data는 그 seqence가 이산적일 수도, 연속적일 수도 있다. 하지만 Neural 구조는 연속적인 데이터라도 이산적인 레이어 구조로 한 스 씩 잘라서 넣어줄 수밖에 없다. 따라서 데이터와 구조 간 miss matching이 나타난다. neural ODE는 연속적인 데이터를 연속적으로 처리하고자 하는 방법이다. 이는 동역학에서 얻은 힌트로, 동역학이란 물체의 변화(미분)로부터 전체적인 운동(본 함수)을 찾아가는 과정이다.

-> 참고 : 미분은 어떠한 점에서의 기울기, 변화율로 볼 수 있다. 적분은 미분의 역관계로 본래의 function을 찾아가는 function approximation이다.
Residual network가 동역학과 닮은 점이 있다. Residual의 학습은 hidden state 간의 변화량에 초점을 두고 있다. 동역학이 순간의 변화로부터 전체 함수를 찾으려 했듯이 Residual network도 hidden state 간의 변화로부터 전체 함수를 찾아간다.

(3) Euler Method
Euler Method는 ODE를 푸는 ODE solver이다. 하나의 점 A0와 ODE가 주어져 있다고 가정해보자. 즉, 하나의 점과 도함수가 주어진 것이다. original function을 알지 못할 때 이것을 찾아가는 방법이 Euler method다. 이는 함수를 근사화하는 과정이다.

위의 과정을 반복하면 아래처럼 original function에 근사한 선을 구할 수 있다. 기존의 nonlinear한 함수를 linear하게 근사한 것이다. 그러나 delta x(이동하는 스텝)를 매우 짧게 가정하면 더욱 더 nonlinear function에 대한 근사 성능을 높일 수 있다. 아래의 그림을 보면 총 4번의 evaluation이 이루어졌다.

모든 점에 대한 기울기를 그리면 아래와 같다. 이를 slope field라 하며, 마치 파동의 형태로 slope가 이어져 있음을 알 수 있다. [1] Slope field에선 한 포인트에서 1개의 slope만 갖는다. [2] Slope field에서 ODE는 Continuous한 변화를 표현한다.


즉 Initial state와 ODE만을 가지고 original function으로 근사하는 과정이 Euler Method다.
Neural ODE에서는 Euler method가 곧 model의 구조다. (Neural ODE의 forward, backward가 모두 Euler method다.) 사실 function approximation을 수행하는 Euler method는 무수한 더하기에 불과하다.


Euler Method는 첫 스텝 y1에서 마지막 yn으로 변하는 과정을 무수한 더하기로 풀어낸 것이고, 이게 곧 neural ODE의 forward이자 backward다.
[1] 함수가 복잡할수록 앞으로 나아가는 step은 더 잘게 쪼개져야 한다. 그에 따라 연산 cost도 증가한다. [2] Euler method는 고정된 step size를 사용한다. Modern solver들은 고정되지 않음.
2. Neural ODE
(1) Neural ODE는 Res-Net
Euler Method는 변화(미분)에서 본 함수를 찾아가는 과정이다.
Res-Net은 Hidden state의 변화(미분)에서 transformation(본 함수)를 찾아가는 과정이다.


한 가지 차이점이 있다면 Residual network는 각 변화, transformation의 step이 discrete한 layer 구조다. 반면 Neural ODE는 그 과정을 연속적인 흐름으로 본다.


Residual network의 forward는 input x가 들어가서 layer들을 거쳐 y로 가는 이산적인 과정으로 변화를 계산한다. Neural ODE는 이와 달리, Euler method와 같은 ODE solver로 풀면 그것이 곧 forward다. 한 번 풀면 끝이다.
(2) Forward and backward of Neural ODE
적분을 계산하는 것으로 순전파, 역전파를 대신하게 된다. 역전파일 때는 input으로 gradient가 들어간다.
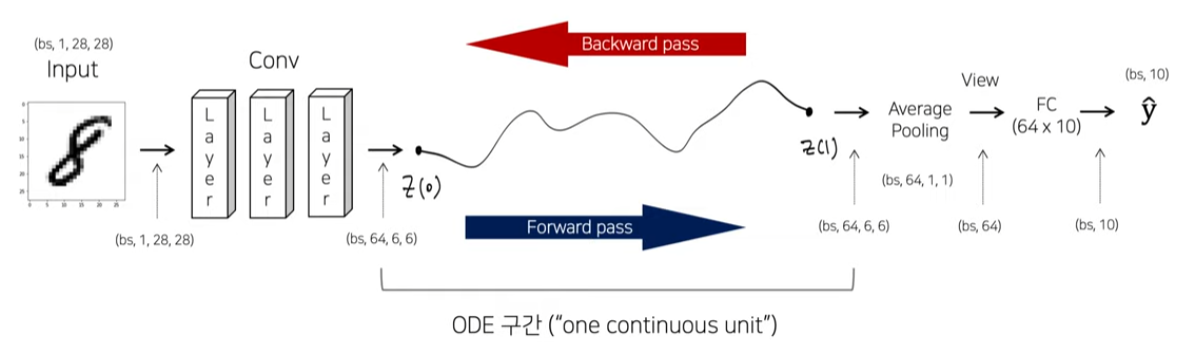
실제로 MNIST data를 학습시킨다 했을 때 [1] input을 넣고 convolution block을 한 번 넣어서 down sampling을 거진다. [2] 이렇게 얻은 feature를 ODE로 순전파한 뒤에 최종 레이블 값까지 계산한다. [3] 역전파도 마찬가지로 z(1)의 gradient를 구한 뒤 ODE를 풀어주면 z(0)의 gradient와 전체의 gradient가 계산 가능하다.
(3) Neural ODE의 특징
[1] Backpropagation을 위해 중간 값들을 유지할 필요가 없다. 즉 memory cost가 낮다. [2] 같은 차원 안에서 연속적인 flow가 이루어진다. 차원이 해당 ODE 안에서 고정된 채로 변화가 진행되므로 Input, Output, 변화 과정 모두 동일 차원이다.
한 포인트에서 1개의 slope만 갖고, 고정된 차원 속에서 진행되므로 ODE가 풀지 못하는 함수가 존재한다. 2개의 initial point에서 시작해 교차하는 함수를 표현할 수 없다. 이에 대한 대책으로는 차원을 증가시켜 교차하는 함수를 풀어 나가는 Augmented Neural ODE가 있다.
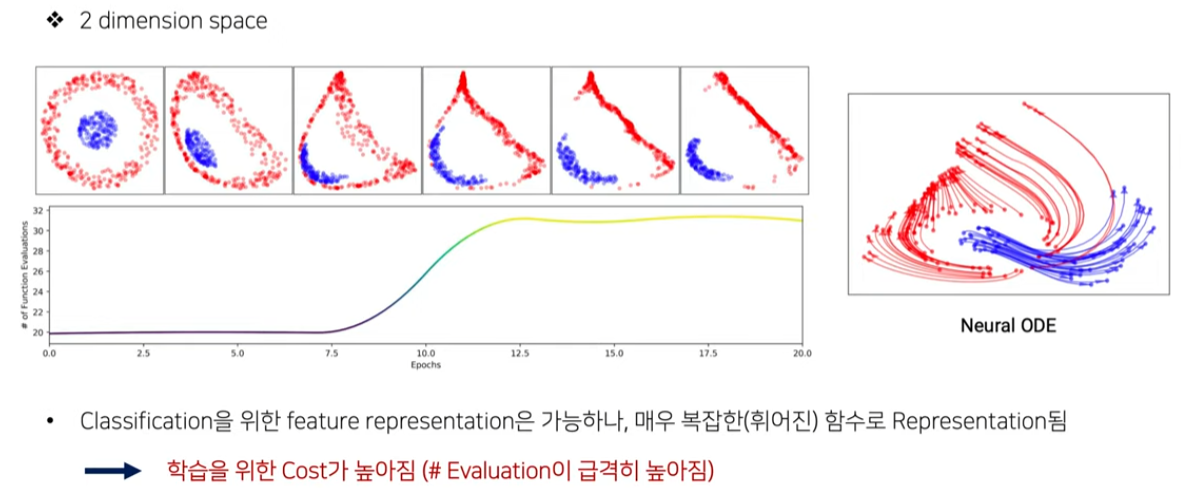
출처: https://www.youtube.com/watch?v=AxJX5eiUVTI
'LAB > 생성형 AI' 카테고리의 다른 글
| 생성모델(3) Denoising Diffusion Implicit Models(DDIM) (1) | 2024.01.08 |
|---|---|
| 생성모델(1) Denoising Diffusion Probabilistic Models(DDPM) (2) | 2024.01.08 |
| 생성모델(5) conditional generation (0) | 2023.12.28 |
| 생성모델(4) Score-based generative models (2) | 2023.12.28 |
| Diffusion_Toy Simulation code 분석 (0) | 2023.07.12 |



