
DQN(2013) -> A2C, A3C(2016) -> DDPG(2015) -> PPO(2017) -> TD3, SAC(2018) 순서.
1. PPO
(1) TRPO (on-policy 알고리즘)
주어진 데이터를 가지고 현재 policy를 최대한 큰 step만큼 빠르게 향상시키면서도, 너무 큰 step으로 업데이트하는 것을 억제하고자 한다. 아래는 PPO과 TRPO의 최적화식이다. TRPO에서는 전자 항을 최대화하면서 후자 항을 최소화하는 것을 목표로 한다. [1] 목적식을 통해 policy의 improvement step을 최대화한다. [2] 이와 동시에 KL divergence를 통해 기존 정책과 새 정책 간의 거리를 제한한다.
step size가 많다고 해서 무작정 좋은 것이 아니다. TRPO는 성능이 떨어지지 않을 것이라고 신뢰할 수 있는 업데이트 범위를 Trust region으로 정의한 후, step size를 Trust region으로 제한하여 안정적으로 데이터 효율성을 향상시킨다.

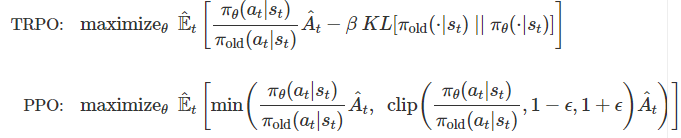
(2) PPO (on-policy 알고리즘)
정책이 과도하게 업데이트되는 문제를 해결하기 위해 고안되었다. 역시 policy gradient 계열의 알고리즘으로, 우수한 성능과 간단한 구현을 보인다. TRPO와 동일한 목적을 가지며, KL divergence 대신 clipping 방식으로 변경하였다. 이를 통해 second-order method가 아닌 first-order method로 계산이 가능해져 실용성을 보인다.
또한 PPO는 Surrogate Objective, 기존 목적 함수를 대체한 목적 함수를 사용한다. Surrogate 목적 함수는 크게 세 가지로 구성된다. [1] πθ란 Actor 네트워크의 가중치 θ로 파라미터화된 정책을 말한다. 업데이트 후의 정책을 의미한다. [2] πθold란 업데이트 전의 정책을 의미한다. [3] At는 advantage를 의미한다.
[[사진 !!]]
Surrogate Objective를 최대화하면? 업데이트 전 정책과 업데이트 후 정책의 비율이 커지게 된다. 즉, 업데이트 전 정책과 업데이트 후 정책의 차이가 커진다는 의미다. -> 아무런 제한 없이 목적 함수를 최대화하면 정책이 과도하게 업데이트될 가능성이 있다는 것을 의미한다. -> 따라서 PPO는 목적 함수에 제한 조건을 추가하여 이 문제를 해결하였다.



clip 연산이 들어간 목적 함수다. Clipped Surrogate Objective란 clip 연산이라는 제한 조건을 추가하여 기존 목적 함수를 대체한 목적 함수이다. clip 연산이란 입력된 값이 지정된 범위를 벗어나게 하지 못하도록 막아주는 연산이다. 예를 들어, clip(0.7, 0.8, 1.2)가 있다면 0.8과 1.2의 범위 내에 들지 못하므로 입력값 0.7은 0.8로 변한다. 당연히 범위 안에 값이 있는 경우, 그 값이 유지된다. PPO에서도 clip 연산의 제한 범위는 0.8, 1.2다.
-> clip 연산은 업데이트 전 정책과 업데이트 후 정책의 비율을 0.8에서 1.2 사이의 값, 즉 1 근처의 값으로 제한한다. 이는 업데이트 전 정책, 후 정책 간의 차이가 크지 않음을 의미하며 PPO는 clip 연산을 통해 정책이 과도하게 업데이트되는 것을 방지한다.
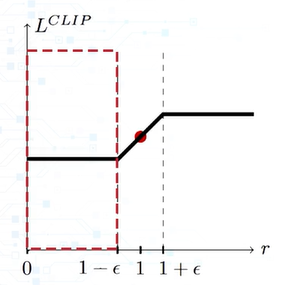
-> PPO 목적 함수의 min은 위와 같이 r이 1- ε보다 작은 경우에 필요하다. 해당 경우는 advantage가 0보다 크기 때문에 r이 커져야 하는데, 오히려 줄어든 경우다. gradient를 통해 다시 목적 함수를 최대화하는 방향으로 업데이트해야하지만, clip 연산 때문에 gradient가 0이 되어 업데이트되지 않는다. min을 사용하면 r이 1- ε보다 작은 경우에 clip 연산을 사용하지 않고 그래디언트 업데이트가 가능하다.

-> PPO의 정책이 업데이트되는 크기를 제한하기 위해선 KL 발산이 사용된다. 이는 두 확률분포 간의 차이를 계산하는 데 사용되는 함수다.
-> 참고로 PPO에서는 1-step TD와 Monte Carlo 방법의 단점을 보완한 'n-step TD' 방법을 고안하였다. 이는 리턴을 n-step까지만 계산해서 분산과 편향을 제어하는 방법이다. PPO에서 advantage를 추정할 때 사용하는 방법은 'Generalized Advantage Estimation'으로, 특정 n-step의 advantage를 계산하는 것이 아니라 모든 step의 advantage를 계산한 후에 가중 합산하는 방법이다.


알고리즘의 학습 과정이다.
Clipping에 대해 자세히 알아보자. Policy의 과도한 업데이트를 막기 위해 사용하는 방법으로, 보상함수 rt(θ)를 '특정 행동을 취한 old policy와 new policy의 확률 비율'로 치환할 수 있다. 그렇기 때문에 policy가 업데이트되지 않은 경우, rt(θ) = 1이 된다. clipping은 rt(θ)를 [1- ε, 1+ ε] 사이로 제한하여, 정책이 업데이트된다 하더라고 특정 action을 수행할 확률이 급격히 변하지 않게 한다.

advantage가 양수일 때는 1+ ε, 음수일 때는 1- ε에 의해서만 clipping이 발생한다. 다시 말하자면 한번에 너무 많은 L CLIP이 증가하는 방향으로 policy가 업데이트되는 것을 피하고자 한다.
PPO는 on-policy 계열의 알고리즘임에도 불구하고 데이터를 재사용할 수 있다. on-policy 정책들의 경우, 업데이트 전의 정책과 업데이트 후의 정책의 차이가 있기에 데이터를 재사용할 수 없다. 그러나 PPO의 경우, 업데이트 전 정책과 후 정책 간의 차이가 크지 않으므로 데이터 재사용이 가능하다. 이를 Importance sampling이라 한다. 기댓값을 계산할 때 기존의 확률분포에서 샘플링하는 것이 아니라 다른 분포에서 샘플링하고자 할 때 사용하는 방법이다. pθold로 샘플링해준다면, 기댓값을 확률분포 pθold를 통해 계산할 수 있기 때문에 업데이트 전 정책으로 얻은 데이터를 학습에 사용할 수 있다.
참고로 Surrogate Objective는 제약 조건이 있지만, clip 연산이 없다. PPO의 목적 함수는 제약 조건이 없지만, clip 연산이 있는데, 이는 PPO가 제약 조건을 clip 연산을 통해 목적 함수에 포함시켰기 때문이다. 즉 PPO는 surrogate Objecitve의 제약 조건을 clip 연산으로 대체한 알고리즘이다.
2. DDPG
(1) DPG
stochastic policy는 행동에 대한 확률 분포를 의미한다. deterministic policy는 하나의 행동에 대한 확률만을 가진다. deterministic policy는 행동을 파라미터화할 수 있으며, 연속적인 행동을 나타낼 수 있다는 장점을 가진다.

Policy gradient 알고리즘의 목표는 목적 함수를 최대화하는 정책을 직접적으로 찾는 것이다. Stochastic Policy Gradient는 목적 함수의 그래디언트를 계산해서, 이에 따라 정책 파라미터 θ를 조절하는 알고리즘이다. 적분이 기대값 형태로 함축되어 연산이 크게 준다는 점에서 실용적이다. 또한 식에 있는 행동-가치 함수인 Qπ(s,a)를 추정하는 방법으로는 monte-carlo policy gradient algorithm(같은 정책을 여러 번 수행, 이중 return을 샘플링해서 Q값 계산)을 사용한다. 기존의 Policy Gradient Theorem을 deterministic policy인 경우로 확장하면 아래 수식과 같다.
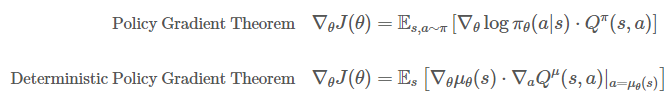
(2) DDPG
DPG에 DQN을 결합한 알고리즘이다. DDPG는 DQN의 부분들을 continous action 영역으로 확장하고자 한다. DDPG는 actor-critic 방식으로 파라미터화된 Q함수를 구한다.

1. 주어진 상태 st에서 정책 네트워크, OU 과정을 통해 행동 at를 획득한다.
2. 선택된 행동을 환경에 수행하여 transition et = (st, at, rt, st+1)을 획득한다.
3. 획득한 trainsition은 replay buffer에 저장하고,
임의의 transition들을 replay buffer에서 샘플링한다.
4. 샘플링된 transition들을 이용하여 TD error를 감소시키는 방향으로 critic을 학습한다.
5. 샘플링된 transition들을 이용하여 DPG를 계산하여 actor를 학습한다.
6. 2개의 타겟 네트워크 파라미터의 soft update를 수행한다.
(*) critic : value network, actor : policy network

[1] Off-policy 방식으로 학습한다. 즉 target policy와 behavior policy가 같지 않아도 학습이 가능하다. 데이터 재사용이 가능하다. 과거의 행동 정책으로 생성한 샘플을 통해 현재의 타겟 정책 업데이트가 가능하다. [2] DQN 기법을 도입하였다. off-policy 알고리즘이므로 샘플 효율성을 극대화시키기 위해 experience replay가 사용될 수 있다. 또한 학습 안정성을 위해 타겟 네트워크가 사용된다. DQN과 다르게 'soft update' 방식으로 타겟 네트워크를 업데이트한다. [3] OU(Ornstein Uhlenbeck) process이다. 연속적인 행동 영역에서의 exploration(탐험)을 효과적으로 수행하기 위해 해당 과정으로 생성된 random noise를 행동에 더해주는 방식을 사용한다. [4] Batch normalization을 사용하여 다양한 연속적인 행동 문제를 효과적으로 학습한다.
3. TD3
DDPG와 거의 같은 형태를 가진다. 여느 actor-critic에도 적용 가능하다. Q값 함수를 2개 학습하고, 정책 업데이트 중에 최고 가치 함수 추정값을 사용한다. 또한 Q함수보다 덜 빈번하게 정책과 타겟을 업데이트한다. 정책을 업데이트할 때 타겟 action에 잡음을 추가함으로써 정책이 너무 높은 값의 Q값 행동을 악용하지 않게끔 한다.

기존의 DDPG와 다르게 critic의 첫번째 층의 input으로 state, action 모두를 받도록 하였다.
출처1: https://talkingaboutme.tistory.com/entry/RL-Review-Deterministic-Policy-Gradient-Algorithm (policy gradient 설명 최고, 혼자서 막막 해보자)
출처3: https://kr.mathworks.com/help/reinforcement-learning/ug/td3-agents.html
'LAB > RL, IRL' 카테고리의 다른 글
| 강화학습(6) 강화학습에 대한 모든 것 : 총 정리ing (0) | 2024.02.15 |
|---|---|
| 강화학습(8) GAIL 실행하기 (LINUX) (1) | 2024.02.01 |
| 강화학습(4) Actor-critic, A2C, A3C, SAC (0) | 2024.01.30 |
| 강화학습(3) 코드 실습 : Q-learning, DQN (0) | 2024.01.30 |
| 강화학습(2) DQN, Double DQN, Deuling DQN (1) | 2024.01.30 |



