kinematic constraints of individual wheels
앞서 Kinematics(2)에서 설명한 approach to kinematic modeling(운동학적 모델링 접근법)은
간단한 경우, [구성요소 휠 속도가 주어진 로봇]의 움직임에 대한 정보를 제공할 수 있다.
그러나 우리는 각 로봇 chassis 설계에 대해 가능한 모션 공간을 결정하고자 한다.
-> 즉 [각 바퀴에 의해 부과되는, robot motion에 대한 제약]을 공식적으로 설명할 것이다.
-> 다양한 휠 형식이 있고, 그에 대한 제약 조건들이 있다.
이를 설명한 후 [이러한 제약 조건이 주어진 로봇의 특성], [작업 공간을 분석하기 위한 도구]를 공부하자.
(0) 개별 휠의 움직임에 대한 제약
[로봇 전체의 움직임을 계산하기 위해] 개별 휠의 움직임은 나중에 결합될 수 있다.
-> 운동학적 특성을 가진 4가지의 기본 휠 유형이 있다.
-> 각 휠 유형에 특정한, 일련의 제약 조건을 제시하는 것으로 시작하자.
<단순화>
-> 휠 평면은 항상 수직으로 유지된다. 휠, 접지면 사이에 단일 접점이 하나씩 존재한다.
-> 그 단일 접점에서는 미끄러짐이 없다고 가정한다.
(바퀴는 [순수한 롤링], [접점을 통해 수직축을 중심으로 회전]라는 조건에서만 motion을 겪는다.)
<제약 조건>
-> [적절한 방향으로의 움직임]이 발생할 때, [휠이 굴러야 한다]는 rolling contact의 개념 탑재.
-> 횡방향(가로 방향)의 미끄러짐이 없다.
즉, 휠이 휠 평면에 직각으로 미끄러지면 안 된다.
(1) Fixed standard wheel
고정 표준 휠에는 [조향을 위한 수직 회전축]이 없다.
-> 따라서 chassis에 대한 각도는 고정되어 있다.
-> 휠 평면을 따라 앞뒤로 움직이고, 접지면과의 접점을 중심으로 회전하는 것으로 제한된다.


그림에 보이는 A의 위치는, 거리 l과 각도로 인한 [극좌표]로 표현된다.
chassis에 대한 휠 평면의 각도는 β(베타)로 표현되며, 고정 표준 휠은 조향할 수 없기 때문에 고정된다.
반지름이 r인 휠은 시간이 지남에 따라 회전할 수 있으므로
수평 축 주위의 회전 위치는 시간 t에 대한 함수이다.
** [휠 평면의 방향을 따라 움직이는 all motion들]은
[접점에서 순수한 롤링이 발생되기 위해, 적절한 양의 휠 스핀이 수반]됨으로써 발생한다.

-> 첫번째 항은, 휠 평면을 따른 총 움직임을 나타낸다.
-> 왼쪽 : 벡터의 세 요소는 각각 [휠 평면을 따라 움직이는] [x, y, θ로부터의 mapping]을 나타낸다.
-> 오른쪽 : [전역 좌표계에 있는 motion parameters]를 [local 좌표게에 있는 motion parameters]로 변환해준다.
(방정식의 다른 모든 parameter, 매개변수가 로봇의 local 좌표계와 관련이 있다. 따라서 필수적인 부분이다.)
-> 두번째 항은, 휠을 회전시킴으로써 달성되는 운동이다.

-> 예를 들어, 바퀴 A가 그러한 위치에 있다고 가정해보자.
-> 휠의 접점이 [Y1과 평행한 방향의 휠 평면]에 [X1]으로 배치된다.
-> 이는 X1을 따라 움직이는 성분을 0으로 제한한다.
-> (X1과 XR이 평행하기 때문에) 휠이 옆으로 미끄러지는 것을 제한한다.
(2) Steered standard wheel
additional degree of freedom이 있다.
-> 휠은 [휠 중심과, 평면과의 접점을 통과하는 수직축]을 중심으로 회전할 수 있다.

-> 조향된 표준 휠에 대한 위치 방정식이다. (하나의 예외를 제외하곤 (1)과 동일)
로봇 chassis의 휠 방향은 더 이상 단일 고정 값 β(베타)가 아니다. 시간 함수에 따라 달라진다.

ϕ'와 달리, β(베타)는 로봇의 순간적인 움직임 제약에 직접적인 영향을 미치지 않는다.
-> 시간 경과에 따른 적분을 통해서만, [스티어링 각도의 변화]가 [차량의 이동성]에 영향을 미칠 수 있다.
(그러니까 그냥 [β관련식 = 0]라고 면 안 되고, [β관련식의 적분 = 0]이라는 방정식을 풀라는 의미)
** 이것은 [스티어링 위치의 변화, β]와 [휠 스핀의 변화, ϕ'] 사이의 매우 중요한 차이다.
(3) Castor wheel

-> 수직 축을 중심으로 조향할 수 있다.
(2)와 달리, [캐스터 휠의 수직 회전축]은 지면 접점을 통과하지 않는다.
(무슨 말이냐면, 그냥 오른쪽 그림처럼 바퀴가 저렇게까지 자유분방하게 움직인다는 의미)
-> [휠과 평면 간의 접점]이 A가 아니라 B point임을 알 수 있다.
-> 추가 파라미터, d가 필요하다. d는 간단히 A과 B 사이의 거리라고 보면 된다.
(2)와 마찬가지로, 캐스터 휠에는 시간의 함수로 변화하는 2개의 매개변수가 있다.
-> ϕ(t) : 시간에 따른 wheel spin(휠 스핀)을 나타낸다.
-> β(t) : 시간에 따른 AB의 조향 각과 방향을 나타낸다.
롤링 제약 조건은 이전과 동일하다.
-> [휠 평면과 나란히 이동할 때] 오프셋 축이 아무런 역할을 하지 않기 때문이다.

그러나 sliding constraint는 달라진다.
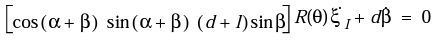
'LAB > Kinematics' 카테고리의 다른 글
| Kinematics(2) - Mobile Robot Kinematics (0) | 2023.02.16 |
|---|---|
| Kinematics(1) - Kinematics Equations (0) | 2023.02.07 |

