Kinematics(1) - Kinematics Equations

 

 

Introduction

 

Kinematics는 물체의 움직임을 다루는 역학의 하위 분야이다. 

 

Industrial, Mobile robot kinematics 둘 다 정방향 및 역방향 운동학에 관심이 있다. 

그러나 모바일 로봇의 경우, encoder values가 고유한 robot poses에 매핑되지 않는다. 

-> 모바일 로봇은 환경에 대해 제한 없이 이동할 수 있다. 

 

로봇의 위치를 직접적으로 측정할 수 있는 방법은 없다. instantaneous way는 없다. 

위치는 선택한 경로에 의존하여, 시간이 지남에 따라 통합되어야 한다. 

위치(동작) 추정치가 부정확해질 수 있다. 

-> 모바일 로봇의 모션을 이해하기 위해선 로봇의 mobility에 배치된 wheel 제약 조건부터 이해해야 한다. 

 

 

Variable Overview

 

robot- state는 [x y θ] 라는 세 가지 element vector로 구성된다. 

• x: Global vehicle x-position in meters (차량의 x 위치)
• y: Global vehicle y-position in meters (차량의 y 위치)
• θ: Global vehicle heading in radians (라디안 단위로 차량 방향 지정)

 

unicycle(외발 자전거), bicycle(자전거), 다른 drive model들은 일반화된 제어 입력 뿐만 아니라 아래 값들도 가진다.

• v: Vehicle speed in meters/s (차량 속도, 미터/초)
• ω: Vehicle angular velocity in radians/s (차량 각속도, 라디안/s)

 

Ackermann 키네마틱스의 경우, steering angle(조향 각도)도 상태에 포함된다. 

-> 조향각(steering angle)이란, 자동차의 직선 주행 위치에서 핸들을 꺾은 각을 말한다. 

    핸들을 꺾은 각에 대해 실제로 타이어가 돈 각을 실조향각이라고 한다. 

• ψ: Vehicle steering angle in radians

 

그 외에도 키네마틱스 방정식엔 다양한 변수들이 존재한다. 

• r: Wheel radius in meters (휠 반경, 미터)
• ˙ϕ: Wheel speed in radians/s (휠 속도, 라디안/s)
• d: Track width in meters (트랙 너비, 미터)
• l: Wheel base in meters (휠 베이스, 미터)

 

Unicycle Kinematics

 

외발 자전거 운동학 방정식은

[unicycle Kinematics 객체를 사용하여, 중심축을 중심으로 회전하는] 단일 롤링 휠을 모델링한다. 

-> unicycle model state는 [x y θ] 이다. 

 

 

우리는 wheel speed 또는 vehicle speed(차량 속도), 헤딩 속도만 입력할 수 있다.

이러한 입력의 변화는 아래의 방정식에도 영향을 미친다.

 

Wheel speed Equation

 

일반화된 입력이 속도 v=r˙ϕ로 주어지고, 방향 각속도 ω로 주어지면 방정식은 아래의 식으로 단순화된다. 

 

Vehicle speed and Healing rate equation(일반화)

 

 

Bicycle Kinematics

 

자전거 운동학 방정식은 

[bicycle Kinematics 객체를 사용하여, 전방 steering 각도를 제어 입력으로 받아들이는] 자동차와 같은 차량을 모델링한다. 

-> bicycle model state는 [x y θ] 이다. 

 

 

우리는 vehicle speed(차량 속도)를 steering 각도, 또는 헤딩 속도로 입력할 수 있다. 

이러한 입력의 변화는 아래의 방정식에도 영향을 미친다.

 

Steering angle Equation

 

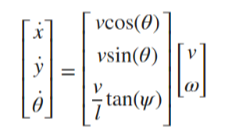
일반화된 형식에서 헤딩 속도 ω는 [관계 ω = v/l*tanψ] 인 조향 각도 ψ와 관련된다. 

방정식은 아래의 식으로 단순화된다. 

 

Vehicle speed and Heading rate equation(일반화)

 

 

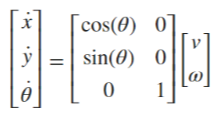
Differential Drive Kinematics

 

다른 드라이브 운동 방정식은 

[differential Drive Kinematics 객체를 사용하여 좌측 및 우측 휠이 독립적으로 회전할 수 있는] 차량을 모델링한다.

-> differential drive model state는 [x y θ] 이다. 

 

 

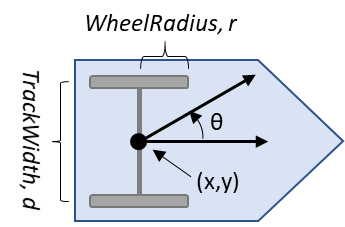
우리는 wheel speed(휠 속도)를 steering 각도, 또는 헤딩 속도로 입력할 수 있다.

이러한 입력의 변화는 아래의 방정식에도 영향을 미친다.

 

Wheel speed Equation

 

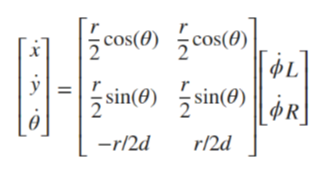
일반화된 형식에서 입력은 [속도 v = r/2*(˙ϕR+˙ϕL)]와 [차량 방향 각속도 ω = r/2d*(˙ϕR−˙ϕL)]로 주어진다. 

방정식은 아래의 식으로 단순화된다. 

 

Vehicle speed and Heading rate equation(일반화)

 

 

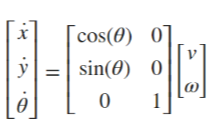
Ackermann Kinematics

 

Ackermann 키네마틱 방정식은

[ackermann Kinematics 객체를 사용하여 아커만 조향 메커니즘을 가진 자동차와 같은] 차량 모델을 모델링한다. 

-> 이 방정식은 타이어가 동심원을 따르도록 (트랙 폭을 기준으로) 액슬 타이어의 위치를 조정한다. 

    수학적으로, 입력이 steering 방향 각속도여야함을 의미한다. 

-> 일반화된 형식은 없다. 

-> differential drive model state는 [x y θ ψ] 이다. 

 

 

For the Ackermann kinematics model, the ODE is ..

 

Kinematic Equations

 

 

 

 

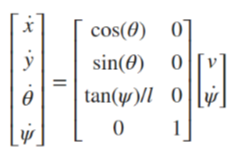
출처:

https://kr.mathworks.com/help/robotics/ug/mobile-robot-kinematics-equations.html

Mobile Robot Kinematics Equations - MATLAB & Simulink - MathWorks 한국