Picture of 회전행렬

by wikipedia.org
좌표축을 기준으로 회전변환을 하려면
(1) 기준이 되는 좌표를 구하자.
(2) 얼마나 회전을 할 지 정하자.
(3) 시계 방향, 반시계 방향과 같은 회전 방향을 정하자.
예시
z축을 기분으로 xy 평면 위의 벡터를 회전시키자. (z성분은 변화가 없다.)
-> x, y,를 2차원 좌표계로 옮겨서 회전시키면 쉽게 이해가 간다.
-> 회전에 대해서는 극좌표계를 사용하자.
(회전을 하더라도 원점과 v 사이의 거리가 달라지지는 않으므로 아래와 같이 표현한다.)
-> (θ, l) = (축과 이루는 각, 원점까지의 거리) 로 표현 가능

좌표를 삼각함수를 이용하여 나타내면 아래와 같다.


z축을 그려서 2차원 공간 -> 3차원 공간으로 만든다.
그리고, 각 θ만큼 벌어진 지점을, 각 α만큼 더 회전시킨다.
wx, wy는 아래와 같이 나타낼 수 있다.

sin법칙, cos법칙을 활용하여
vx, vy와 wx, wy 사이의 관계를 구할 수 있다.
-> cos 법칙 : cos(a+b) = cosa*cosb - sina*sinb
-> sin 법칙 : sin(a+b) = sina*cosb + cosa*sinb

z축을 기준으로 a만큼 회전시키는 변환식은 아래와 같이 도출된다.
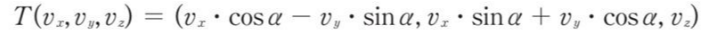
i, j, k라는 단위행렬이 다음과 같으므로
전체 회전행렬은 다음과 같이 표현할 수 있다.

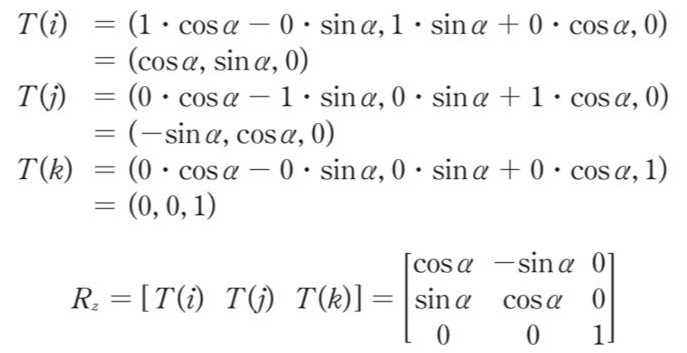
이와 같은 원리로, 회전행렬을 구할 수 있다.
-> [z축 기준 회전] = [z축 성분은 바뀌지 않음] = [3행의 component들이 저런 형식임]
회전변환의 역행렬
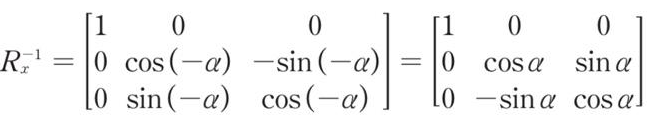
회전변환의 역행렬을 살펴보면, 둘이 서로 orthogonal matrix(직교 행렬)임을 알 수 있다.
-> 직교 행렬 : 열 벡터 또는 행 벡터들이 서로 orthonormal(정규 직교)인 경우
-> 정규 직교 : 두 벡터의 길이가 모두 1, 서로 수직(= 내적한 값이 0)인 경우
출처: